题目内容
10.等比数列{an}中,a1+a7=65,a3a5=64,且an+1<an.(1)求{an}的通项公式;
(2)求{an}的前5项的和S5.
分析 (1)设公比为q,由a3•a5=64,可得a1•a7=64.又a1+a7=65,an+1<an.即可解出q,利用通项公式即可得出;
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)设公比为q,∵a3•a5=64,∴a1•a7=64.
又a1+a7=65,an+1<an.
解得a1=64,a7=1.
∴64×q6=1,
解得q=$\frac{1}{2}$.
∴an=$64×(\frac{1}{2})^{n-1}$=2n+5.
(2)S5=$\frac{64×(1-\frac{1}{{2}^{5}})}{1-\frac{1}{2}}$=124.
点评 本题考查了本题考查了等比数列性质通项公式及其的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是( )
| A. | x与y负相关,x与z负相关 | B. | x与y正相关,x与z正相关 | ||
| C. | x与y正相关,x与z负相关 | D. | x与y负相关,x与z正相关 |
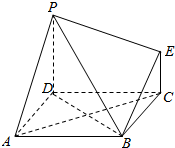 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且