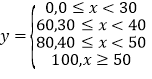题目内容
【题目】判断下列命题中p是q的什么条件.(充分不必要条件必要不充分条件,充要条件,既不充分也不必要条件)
(1)p:数a能被6整除,q:数a能被3整除;
(2)![]() ,
,![]() ;
;
(3)![]() 有两个角相等,
有两个角相等,![]() 是正三角形;
是正三角形;
(4)若![]() ,
,![]() ,
,![]() ;
;
(5)![]() ,
,![]() .
.
【答案】(1)p是q的充分不必要条件(2)P是q的充分不必要条件(3)p是q的必要不充分条件(4)p是q的充要条件(5)p是q的既不充分也不必要条件
【解析】
判断两个命题![]() 和
和![]() 是否正确,然后得结论.
是否正确,然后得结论.
解析(1)因为“数a能被6整除”能推出“数a能被3整除”,所以![]() ,
,
但“数a能被3整除”推不出“数a能被6整除”,如![]() ,所以
,所以![]() ,所以p是q的充分不必要条件.
,所以p是q的充分不必要条件.
(2)因为![]() 能推出
能推出![]() ,即
,即![]() ;但当
;但当![]() 时,如
时,如![]() ,推不出
,推不出![]() ,即
,即![]() ,所以P是q的充分不必要条件.
,所以P是q的充分不必要条件.
(3)因为“![]() 有两个角相等”推不出“
有两个角相等”推不出“![]() 是正三角形”,因此
是正三角形”,因此![]() ,但“
,但“![]() 是正三角形”能推出“
是正三角形”能推出“![]() 有两个角相等”,即
有两个角相等”,即![]() ,所以p是q的必要不充分条件.
,所以p是q的必要不充分条件.
(4)若![]() ,则
,则![]() ,即
,即![]() ;若
;若![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() ,所以p是q的充要条件.
,所以p是q的充要条件.
(5)当![]() ,
,![]() 时,
时,![]() 推不出
推不出![]() ,知
,知![]() ,又当
,又当![]() ,
,![]() 时,
时,![]() 推不出
推不出![]() ,知
,知![]() ,所以p是q的既不充分也不必要条件.
,所以p是q的既不充分也不必要条件.

练习册系列答案
相关题目
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: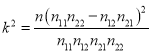 ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.