题目内容

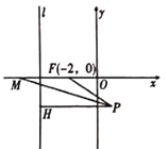
【题目】已知椭圆的左、右焦点分别为，长轴长为4，且过点.

（1）求椭圆C的方程；

（2）过的直线l交椭圆C于两点，过A作x轴的垂线交椭圆C与另一点Q（Q不与重合）.设的外心为G，求证为定值.

【答案】（1）（2）证明见解析

【解析】

（1）根据长轴及椭圆过点即可求出；

（2）由题意设直线为，联立椭圆方程可求，求出外接圆圆心，计算，化简即可证明为定值.

（1）由题意知，

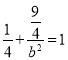将P点坐标代入椭圆方程得，解得，

所以椭圆方程为.

（2）由题意知，直线的斜率存在，且不为0，设直线为，

代入椭圆方程得.

设，则，

所以的中点坐标为，

所以.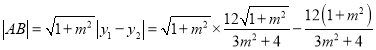

因为G是的外心，所以G是线段的垂直平分线与线段的垂直平分线的交点，

的垂直平分线方程为，

令，得，即，所以，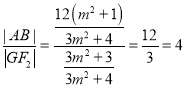

所以，所以为定值，定值为4.

练习册系列答案
相关题目

【题目】在单位圆O：x2+y2＝1上任取一点P（x，y），圆O与x轴正向的交点是A，设将OA绕原点O旋转到OP所成的角为θ，记x，y关于θ的表达式分别为x＝f（θ），y＝g（θ），则下列说法正确的是（　　）

A.x＝f（θ）是偶函数，y＝g（θ）是奇函数

B.x＝f（θ）在为增函数，y＝g（θ）在为减函数

C.f（θ）+g（θ）≥1对于恒成立

D.函数t＝2f（θ）+g（2θ）的最大值为

【题目】如图，在平面直角坐标系中，已知点，直线，过动点作于点，的平分线交轴于点，且，记动点的轨迹为曲线．

（1）求曲线的方程；

（2）过点作两条直线，分别交曲线于两点（异于点）．当直线的斜率之和为2时，直线是否恒过定点？若是，求出定点的坐标；若不是，请说明理由．

【题目】已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

（1）求椭圆C的标准方程；

（2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q.

（i）证明：OT平分线段PQ（其中O为坐标原点）；

（ii）当最小时，求点T的坐标.

【题目】某校开展学生社会法治服务项目，共设置了文明交通，社区服务，环保宣传和中国传统文化宣讲四个项目，现有该校的甲、乙、丙、丁4名学生，每名学生必须且只能选择1项．

（1）求恰有2个项目没有被这4名学生选择的概率；

（2）求“环保宣传”被这4名学生选择的人数的分布列及其数学期望．

【题目】已知函数有两个不同的极值点.

（1）求的取值范围.

（2）求的极大值与极小值之和的取值范围.

（3）若，则是否有最小值？若有，求出最小值；若没有，说明理由.

【题目】已知为抛物线上的一点，，为抛物线上异于点的两点，且直线的斜率与直线的斜率互为相反数.

（1）求直线的斜率；

（2）设直线过点并交抛物线于，两点，且，直线与轴交于点，试探究与的夹角是否为定值，若是则求出定值，若不是，说明理由.

【题目】已知点A，B的坐标分别是（，0），（，0），动点M（x，y）满足直线AM和BM的斜率之积为﹣3，记M的轨迹为曲线E．

（1）求曲线E的方程；

（2）直线y＝kx+m与曲线E相交于P，Q两点，若曲线E上存在点R，使得四边形OPRQ为平行四边形（其中O为坐标原点），求m的取值范围．

【题目】如图，是以为直径的圆上一点，，等腰梯形所在的平面垂直于⊙所在的平面，且.

（1）求与所成的角；

（2）若异面直线和所成的角为，求二面角的余弦值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网