题目内容
【题目】下列结论中错误的是( )
A.设命题p:?x∈R,使![]() +x+2<0,则¬P:?x∈R,都有
+x+2<0,则¬P:?x∈R,都有![]() +x+2≥0
+x+2≥0
B.若x,y∈R,则“x=y”是“xy≤![]() 取到等号”的充要条件
取到等号”的充要条件
C.已知命题p和q,若p∧q为假命题,则命题p与q都为假命题
D.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题
【答案】C
【解析】对于A,命题p:x∈R,使x2+x+2<0,它的否定¬P:x∈R,都有x2+x+2≥0,是正确的;
对于B,若x,y∈R,则“x=y”时,“xy≤(![]() )2取到等号”,
)2取到等号”,
当“xy≤(![]() )2取到等号时”,“x=y”成立,∴是充要条件,命题正确;
)2取到等号时”,“x=y”成立,∴是充要条件,命题正确;
对于C,当命题p∧q为假命题时,命题p、q有1个为假命题,或者都是假命题,∴命题C错误;
对于D,“在△ABC中,A>BsinA>sinB”,∴原命题的逆命题是真命题,是正确的.
故选:C.
【考点精析】利用复合命题的真假和特称命题对题目进行判断即可得到答案,需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真;特称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;特称命题的否定是全称命题.
;特称命题的否定是全称命题.

 习题精选系列答案
习题精选系列答案【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班![]() 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人抽到喜爱打篮球的学生的概率为
人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜爱打篮球与性别有关?说明你的理由;
的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:![]() ,
,![]() )
)
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
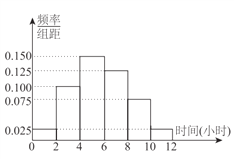
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”

