题目内容
5.已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A、B两点,|AB|=6,P为C的准线上一点,则△ABP的面积为( )| A. | 3 | B. | 6 | C. | 9 | D. | 18 |
分析 首先设抛物线的解析式y2=2px(p>0),写出次抛物线的焦点、对称轴以及准线,然后根据通径|AB|=2p,求出p,△ABP的面积是|AB|与DP乘积一半.
解答 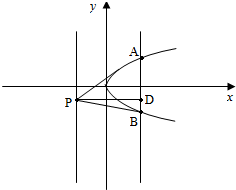 解:设抛物线的解析式为y2=2px(p>0),
解:设抛物线的解析式为y2=2px(p>0),
则焦点为F($\frac{p}{2}$,0),对称轴为x轴,准线为x=-$\frac{p}{2}$
∵直线l经过抛物线的焦点,A、B是l与C的交点,
又∵AB⊥x轴,
∴|AB|=2p=6,
∴p=3,又∵点P在准线上
∴DP=($\frac{p}{2}$+|-$\frac{p}{2}$|)=p=3,
∴S△ABP=$\frac{1}{2}$(DP•AB)=$\frac{1}{2}$×6×3=9,
故选:C.
点评 本题主要考查抛物线焦点、对称轴、准线以及焦点弦的特点;关于直线和圆锥曲线的关系问题一般采取数形结合法.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.直线2x-y-10=0和圆(x-2)2+(y+1)2=3的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 过圆心 |
13.若(x-1)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7,则a1等于( )
| A. | -14 | B. | 448 | C. | -1024 | D. | -16 |