题目内容
已知函数f(x)＝sin2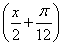
＋
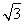sin
－
.
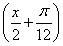
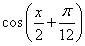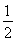(1)在△ABC中，若sin C＝2sin A，B为锐角且有f(B)＝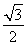
，求角A，B，C；
(2)若f(x)(x＞0)的图象与直线y＝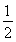
交点的横坐标由小到大依次是x1，x2，…，xn，求数列{xn}的前2n项和，n∈N*.
（1）
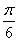（2）(2n2－n)π.
【解析】(1)因为f(x)＝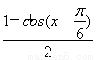
＋
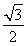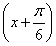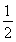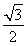sin 
－
＝
sin 
－
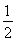cos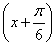 
＝sin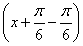 
＝sin x，
又因为f(B)＝
，故sin B＝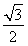
.又B为锐角，所以B＝
.
由sin C＝2sin A，得c＝2a，所以b2＝a2＋4a2－2a·2acos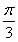 
＝3a2.所以c2＝a2＋b2.所以△ABC为直角三角形，C＝
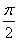，A＝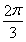
－
＝.
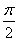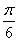(2)由正弦曲线的对称性、周期性，可知
＝
，
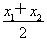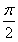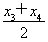＝2π＋
，…，
＝2(n－1)π＋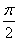
，
所以x1＋x2＋…＋x2n－1＋x2n＝π＋5π＋9π＋…＋(4n－3)π＝nπ＋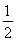
n(n－1)·4π＝(2n2－n)π.
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
