题目内容
已知椭圆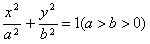 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值不小于
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值不小于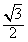 (a-c),
(a-c),
(1)证明:椭圆上的点到F2的最短距离为a-c;
(2)求椭圆的离心率e的取值范围;
(3)设椭圆的短半轴长为1,圆F2与x轴的右交点为Q,过点Q作斜率为k(k>0)的直线l与椭圆相交于A、B两点,若OA⊥OB,求直线l被圆F2截得的弦长S的最大值.
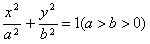 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值不小于
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值不小于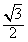 (a-c),
(a-c),(1)证明:椭圆上的点到F2的最短距离为a-c;
(2)求椭圆的离心率e的取值范围;
(3)设椭圆的短半轴长为1,圆F2与x轴的右交点为Q,过点Q作斜率为k(k>0)的直线l与椭圆相交于A、B两点,若OA⊥OB,求直线l被圆F2截得的弦长S的最大值.
解:(1)假设椭圆上的任一点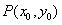 ,则
,则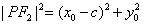 ,
,
由椭圆方程易得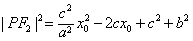 ,
,
显然当x0=a时,|PF2|取最小值a-c;
(2)依题意知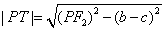 ,
,
当且仅当|PF2|取得最小值时,|PT|取最小值,
∴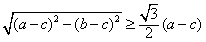 ,
,
又因为b-c>0.得 ;
;
(3)依题意Q点的坐标为(1,0),则直线l的方程为y=k(x-1),
代入椭圆方程得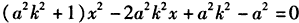 ,
,
设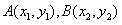 ,
,
则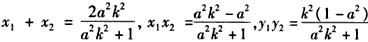 ,
,
又OA⊥OB,∴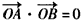 ,即
,即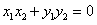 ,
,
∴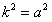 ,即k=a,直线l的方程为ax-y-a=0,
,即k=a,直线l的方程为ax-y-a=0,
圆心F2(c,0)到直线l的距离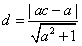 ,
,
由图象可知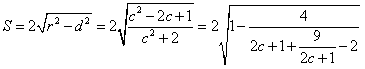 ,
,
由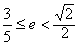 得
得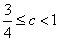 ,
,
∴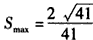 。
。
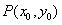 ,则
,则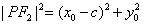 ,
,由椭圆方程易得
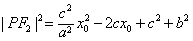 ,
,显然当x0=a时,|PF2|取最小值a-c;
(2)依题意知
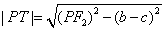 ,
,当且仅当|PF2|取得最小值时,|PT|取最小值,
∴
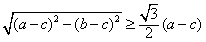 ,
,又因为b-c>0.得
 ;
; (3)依题意Q点的坐标为(1,0),则直线l的方程为y=k(x-1),
代入椭圆方程得
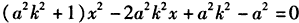 ,
,设
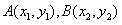 ,
,则
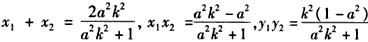 ,
,又OA⊥OB,∴
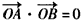 ,即
,即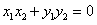 ,
, ∴
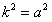 ,即k=a,直线l的方程为ax-y-a=0,
,即k=a,直线l的方程为ax-y-a=0,圆心F2(c,0)到直线l的距离
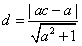 ,
,由图象可知
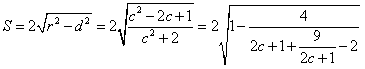 ,
,由
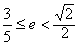 得
得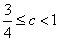 ,
,∴
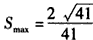 。
。 
练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线