题目内容

已知函数y=sin(x-
π
12
)cos(x-
π
12
)，则此函数图象的一个对称中心是（　　）
分析：由y=sin(x-
π
12
)cos(x-
π
12
)=
1
2
sin(2x-
π
6
 )，令2x-
π
6
=kπ可得x=
kπ
2
+
π
12
，结合选项可得
解答：解：∵y=sin(x-
π
12
)cos(x-
π
12
)=
1
2
sin(2x-
π
6
 )
令2x-
π
6
=kπ可得x=
kπ
2
+
π
12

当k=0时可得函数的一个对称中心为：(
π
12
，0)
故选：A．
点评：本题主要考查了二倍角公式的应用，三角函数性质的应用，属于基础试题．
练习册系列答案
相关题目
已知函数y=|sin（2x-
π
6
）|，则以下说法正确的是（　　）
A、周期为
π
4
B、函数图象的一条对称轴是直线x=
π
3
C、函数在[
2π
3
，
5π
6
]上为减函数
D、函数是偶函数
已知函数y=sin（ωx+φ）（ω＞0，0＜φ＜
π2
），且此函数的图象如图所示，则点（ω，φ）的坐标是
 
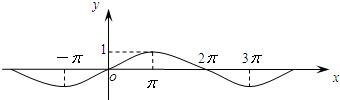．精英家教网
精英家教网已知函数y=sinωx（ω＞0）的图象如图所示，把y=sinωx的图象所有点向右平移
2π
3
个单位后，再把所得函数图象上所有点得横坐标变为原来的
1
2
倍（纵坐标不变），得到函数y=f（x）的图象，则f（x）=
 
．
已知函数y=sin（ωx+1）的最小正周期是
π2
，则正数ω=
4
4
．
已知函数y=sin(2x-
π4
)，
（1）试用五点法作函数在一个周期上的图象；
（2）根据图象直接写出函数的周期和单调递增区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网