题目内容
若 是方程
是方程 2-
2- m
m +m=0的两实根,且
+m=0的两实根,且 、
、 、
、 成等比数列,则实数m的值为
成等比数列,则实数m的值为
 是方程
是方程 2-
2- m
m +m=0的两实根,且
+m=0的两实根,且 、
、 、
、 成等比数列,则实数m的值为
成等比数列,则实数m的值为A. | B.0或 | C.0 | D.2 |
A
此题答案选A
分析:由α、β是方程的两个根,利用为韦达定理表示出两根之和与两根之积,再由α、α-β、β成等比数列,利用等比数列的性质列出关于α与β的关系式,利用完全平方公式变形后,将表示出的两根之和与两根之积代入得到关于m的方程,求出方程的解得到m的值,再把求出的m的值代入方程检验,即可得到满足题意的实数m的值.
解答:解:∵α、β是方程x2- mx+m=0的两实根,
mx+m=0的两实根,
∴α+β= m,αβ=m,
m,αβ=m,
又α、α-β、β成等比数列,
∴(α-β)2=αβ,即(α+β)2=5αβ,
∴10m2=5m,即m(2m-1)=0,
解得:m=0或m=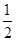 ,
,
当m=0时,方程的解α=β=0,
可得α、α-β、β三式都为0,不成等比数列,故舍去,
则实数m的值为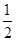 .
.
故选A
分析:由α、β是方程的两个根,利用为韦达定理表示出两根之和与两根之积,再由α、α-β、β成等比数列,利用等比数列的性质列出关于α与β的关系式,利用完全平方公式变形后,将表示出的两根之和与两根之积代入得到关于m的方程,求出方程的解得到m的值,再把求出的m的值代入方程检验,即可得到满足题意的实数m的值.
解答:解:∵α、β是方程x2-
 mx+m=0的两实根,
mx+m=0的两实根,∴α+β=
 m,αβ=m,
m,αβ=m,又α、α-β、β成等比数列,
∴(α-β)2=αβ,即(α+β)2=5αβ,
∴10m2=5m,即m(2m-1)=0,
解得:m=0或m=
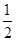 ,
,当m=0时,方程的解α=β=0,
可得α、α-β、β三式都为0,不成等比数列,故舍去,
则实数m的值为
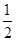 .
.故选A

练习册系列答案
相关题目
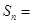 _______
_______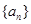 为等比数列,且满足
为等比数列,且满足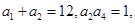 则
则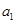 =( )
=( )
 或16
或16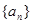 中,
中,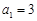 ,前三项和为21,则
,前三项和为21,则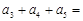 ( )
( )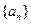 的前n项和为
的前n项和为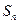 ,若
,若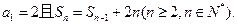
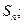
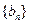 满足
满足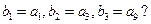 若存在,则求出数列
若存在,则求出数列 中,
中, 则公比
则公比