题目内容
若等比数列{an}满足anan+1=16n,则公比为
| A.2 | B.4 | C.8 | D.16 |
B
令n=1,得到第1项与第2项的积为16,记作①,令n=2,得到第2项与第3项的积为256,记作②,然后利用②÷①,利用等比数列的通项公式得到关于q的方程,求出方程的解即可得到q的值,然后把q的值代入经过检验得到满足题意的q的值即可.
解:当n=1时,a1a2=16①;当n=2时,a2a3=256②,
②÷①得: =16,即q2=16,解得q=4或q=-4,
=16,即q2=16,解得q=4或q=-4,
当q=-4时,由①得:a12×(-4)=16,即a12=-4,无解,所以q=-4舍去,
则公比q=4.
故选B
解:当n=1时,a1a2=16①;当n=2时,a2a3=256②,
②÷①得:
 =16,即q2=16,解得q=4或q=-4,
=16,即q2=16,解得q=4或q=-4,当q=-4时,由①得:a12×(-4)=16,即a12=-4,无解,所以q=-4舍去,
则公比q=4.
故选B

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
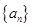 是等比数列,以下哪一个是假命题
是等比数列,以下哪一个是假命题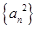 是等比数列 B
是等比数列 B 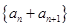 是等比数列
是等比数列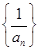 是等比数列 D
是等比数列 D 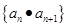 是等比数列
是等比数列 是方程
是方程 2-
2- m
m 、
、 、
、 成等比数列,则实数m的值为
成等比数列,则实数m的值为
 中an>0,且
中an>0,且 ,则
,则 = ( )
= ( )  中,若
中,若 ,
, ,则
,则 ( )
( )

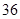

 ,则函数
,则函数 =
= -
- 的值域为
的值域为 ,+∞)
,+∞)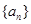 中,
中,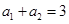 ,
,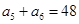 ,则
,则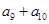 等于( )
等于( )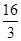
 的前n项和为
的前n项和为 ,若
,若 ,则
,则