Question

【题目】已知函数

（1）判断的奇偶性并证明；

（2）判断的单调性并说明理由；

（3）若对任意恒成立,求的取值范围．

Answer 1

【答案】（1）奇函数,证明见解析；（2）增函数,理由见解析；（3）

【解析】

（1）求出的定义域,再计算与比较,即可判断奇偶性；

（2）对函数求导，判断导函数大于，即可的的单调性；

（3）利用函数的奇偶性和单调性和将转化为，再分情况讨论即可得出的取值范围．

解（1）判断：是奇函数.

证明：因为,定义域为,

所以是奇函数；

（2）判断：在上是增函数.

证明：因为

所以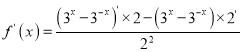

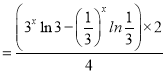
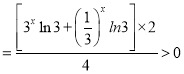
所以在上是增函数.

（3）若对任意恒成立,求的取值范围．

因为所以,

由（1）知是奇函数,则

又由（2）知在上是增函数,则

,对任意恒成立,

①当 时,,符合题意；

②当 时,,

因为，无最小值,所以不合题意；

③当 时,,

则,解得,所以，符合题意；

综上所述：.

故若对任意恒成立，的取值范围为．