题目内容
【题目】若数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将数列
,则将数列![]() 和
和![]() 的距离定义为
的距离定义为![]() .
.
(1)求数列1,3,5,6和数列2,3,10,7的距离.
(2)记![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,数列
的集合,数列![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() .若
.若![]() ,
, ![]() ,数列
,数列![]() 和
和![]() 的距离小于2016,求
的距离小于2016,求![]() 的最大值.
的最大值.
(3)记![]() 是所有7项数列
是所有7项数列![]() (其中
(其中![]() ,
, ![]() 或
或![]() )的集合,
)的集合, ![]() ,且
,且![]() 中的任何两个元素的距离大于或等于3.求证:
中的任何两个元素的距离大于或等于3.求证: ![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
【答案】(1)7;(2)3455;(3)见解析.
【解析】(1)根据题意,将两数列对应代入计算,问题即可得解;(2)由题意,根据递推关系,不难发现数列![]() 是以4为周期的数列,由此可确定数列
是以4为周期的数列,由此可确定数列![]() 亦为周期数列,由其首项即可知对应数列各项,依据定义当项数
亦为周期数列,由其首项即可知对应数列各项,依据定义当项数![]() 越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
越大时,其距离也呈周期性且越大,从而问题可得解;(3)根据题意,这里可以考虑采用反证法来证明,首先假设问题不成立,再通过特殊赋值法,依据定义进行运算,发现与条件相矛盾,从而问题可得证.
试题解析:(1)由题得数列1,3,5,6和数列2,3,10,7的距离为7.
(2)设![]() ,其中
,其中![]() 且
且![]() .
.
由![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,….
,….
所以![]() ,
, ![]() ,….
,….
因此集合![]() 中的所有数列都具有周期性,且周期为4.
中的所有数列都具有周期性,且周期为4.
所以数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
,
数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .
.
因为![]() ,
,
所以项数![]() 越大,数列
越大,数列![]() 和
和![]() 的距离越大.
的距离越大.
因为![]() ,
,
而![]()
![]() ,
,
因此,当![]() 时,
时, ![]() .
.
故![]() 的最大值为3455.
的最大值为3455.
(3)假设![]() 中的元素个数大于或等于17.
中的元素个数大于或等于17.
因为数列![]() 中,
中, ![]() 或1,
或1,
所以仅由数列前三项组成的数组(![]() ,
, ![]() ,
, ![]() )有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
)有且只有8个:(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1).
那么这17个元素之中必有3个具有相同的![]() ,
, ![]() ,
, ![]() .
.
设这3个元素分别为![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() .
.
因为这3个元素中每两个元素的距离大于或等于3,
所以在![]() 与
与![]() 中,
中, ![]()
![]() 至少有3个成立.
至少有3个成立.
不妨设![]() ,
, ![]() ,
, ![]() .
.
由题意得![]() ,
, ![]() 中一个等于0,另一个等于1.
中一个等于0,另一个等于1.
又因为![]() 或1,所以
或1,所以![]() 和
和![]() 中必有一个成立.
中必有一个成立.
同理得: ![]() 和
和![]() 中必有一个成立,
中必有一个成立, ![]() 和
和![]() 中必有一个成立,
中必有一个成立,
所以“![]()
![]() 中至少有两个成立”和“
中至少有两个成立”和“![]()
![]() 中至少有两个成立”中必有一个成立.
中至少有两个成立”中必有一个成立.
故![]() 和
和![]() 中必有一个成立,这与题意矛盾.
中必有一个成立,这与题意矛盾.
所以![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.

 53随堂测系列答案
53随堂测系列答案【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
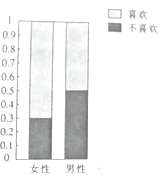
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
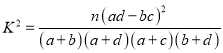 ,其中
,其中![]()