题目内容
在等比数列{an}中,前n项和为Sn,若Sm,Sm+2,Sm+1成等差数列,则am,am+2,am+1成等差数列.(1)写出这个命题的逆命题;
(2)判断逆命题是否为真,并给出证明.
解:(1)逆命题:在等比数列 {an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1成等差数列;
(2)设{an}的首项为a1,公比为q,则2am+2=am+am+1,于是2a1qm+1=a1qm-1+a1qm.
由a1≠0,q≠0,化简上式得2q2-q-1=0,
解得q=1或q=-![]() ,
,
当q=1时,∵Sm=ma1,Sm+2=(m+2)a1,S(m+1)=(m+1)a1,
∴Sm+Sm+1≠2Sm+2,
即Sm,Sm+2,Sm+1不成等差数列;
当q=-![]() 时,∵Sm+Sm+1=
时,∵Sm+Sm+1=
而2Sm+2=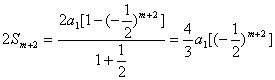 ,
,
∴Sm+Sm+1=2Sm+2,即Sm,Sm+2,Sm+1成等差数列;
综上得,当公比q=1时,逆命题为假,当q=-![]() 时,逆命题为真.
时,逆命题为真.

练习册系列答案
相关题目
在等比数列{an}中,若a1=1,公比q=2,则a12+a22+…+an2=( )
| A、(2n-1)2 | ||
B、
| ||
| C、4n-1 | ||
D、
|