题目内容
14.试证对于任何整数a,数8a+7不是三个整数的平方和.分析 利用反证法证明,分类讨论,即可得出结论.
解答 证明:假设存在任意正整数n,使8a+7是三个正整数的平方和即设三个整数分别为x,y,z,
则有:x2+y2+z2=8a+7
即x2+y2+z2=2﹙4a+3)+1,
则x,y,z有一个奇数,或三个全是奇数,
①若x,y,z中,有一个奇数两个偶数,令x=2n+1,y=2b,z=2c
则4n2+4n+1+4b2+4c2=2﹙4a+3﹚+1,
即4﹙n2+n+b2+c2﹚=2﹙4a+3﹚,
即2﹙n2+n+b2+c2﹚=4a+3
即:一个奇数等于另一个偶数,矛盾;
②若x,y,z都是奇数,
令x=2n+1,y=2b+1,z=2c+1,
则4﹙n2+b2+c2+n+b+c+$\frac{1}{2}$﹚+1=2﹙4a+3﹚+1
4﹙n2+b2+c2+n+b+c+$\frac{1}{2}$﹚=2﹙4a+3﹚,
所以2﹙n2+b2+c2+n+b+c+$\frac{1}{2}$﹚=4a+3,
所以2﹙n2+b2+c2+n+b+c﹚=4a+2,
所以n2+b2+c2+n+b+c=2a+1,
n,b,c都是奇数,偶数个奇数的和是偶数,2a+1是奇数,
即:一个奇数等于另一个偶数,矛盾
综上所述:8a+7不可能是三个整数的平方和
点评 本题考查反证法,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
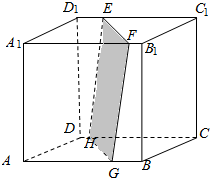 在正方体ABCD-A1B1C1D1中,作截面EFGH(如图所示)交C1D1,A1B1,AB,CD分别于点E,F,G,H,则四边形EFGH的形状是( )
在正方体ABCD-A1B1C1D1中,作截面EFGH(如图所示)交C1D1,A1B1,AB,CD分别于点E,F,G,H,则四边形EFGH的形状是( )