题目内容
【题目】操场上有100个人排成一圈,按顺时针方向依次标为![]() ,
,![]() ,…,
,…,![]() .主持人将编号为l,2,…,50的纪念品按照以下方式依次分发给众人:先将第l号纪念品交给
.主持人将编号为l,2,…,50的纪念品按照以下方式依次分发给众人:先将第l号纪念品交给![]() ;然后顺时针跳过1个人,将第2号纪念品交给
;然后顺时针跳过1个人,将第2号纪念品交给![]() ;再顺时针跳过2个人,将第3号纪念品交给
;再顺时针跳过2个人,将第3号纪念品交给![]() ,……第
,……第![]() 次顺时针跳过
次顺时针跳过![]() 个人,将第
个人,将第![]() 号纪念品交给
号纪念品交给![]() ,其中,
,其中,![]() ,如此下去,直到纪念品发完为止.试求得到纪念品最多的人及其所得纪念品的编号.
,如此下去,直到纪念品发完为止.试求得到纪念品最多的人及其所得纪念品的编号.
【答案】见解析
【解析】
记第![]() 个与第
个与第![]() 个纪念品为同一人所得.则
个纪念品为同一人所得.则![]() ,
,
即![]() .
.
显然,![]() ,且
,且![]() 与
与![]() 的奇偶性不同.
的奇偶性不同.
(1)如果![]() ,则
,则![]() .
.
(i)若![]() ,则
,则![]() .
.
又![]() ,故
,故![]() .
.
所以,![]() ,其中,
,其中,![]() ,1,…,
,1,…,![]() ;
;![]() ,2.
,2.
经计算![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(ii)若![]() ,则
,则![]() .
.
由![]() .
.
故![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)如果![]() ,则
,则![]() .
.
(i)若![]() ,则
,则![]() .
.
故![]() ,
,![]() .
.
(ii)若![]() ,则
,则![]() ,75.
,75.
故![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
综上,![]() 与
与![]() 分别被
分别被![]() 与
与![]() 得到,其余各人至多得到2个纪念品.
得到,其余各人至多得到2个纪念品.

【题目】某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售量y | 1.8 | 3.0 | 4.0 | 4.2 | 5.0 | 5.3 | 5.4 |
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(保留小数点后两位);
(2)若用![]() 模型拟合y与x的关系,可得回归方程
模型拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y-x.根据(2)的结果,当广告费x=20时,求销售量及利润的预报值.
参考公式:回归直线![]() =
=![]() +
+![]() x的斜率和截距的最小二乘估计分别为
x的斜率和截距的最小二乘估计分别为![]() =
=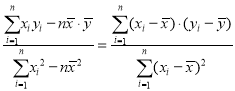 ,
,![]() .
.
参考数据:![]() ≈2.24,
≈2.24,![]() ,
, ![]()
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)请画出性别与休闲方式的![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.10的前提下,认为休闲方式与性别有关?
附: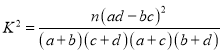 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |