题目内容
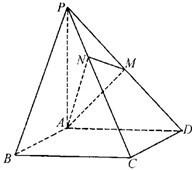如图，已知四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，且PA=AD=2，点M、N分别在侧棱PD、PC上，且PM=MD．（1）求证：AM⊥平面PCD；
（2）若
| PN |
| 1 |
| 2 |
| NC |
分析：（Ⅰ）欲证AM⊥平面PCD，根据直线与平面垂直的判定定理可知只需证AM与平面PCD内两相交直线垂直，根据线面垂直的性质可知CD⊥AM，根据等腰三角形可知AM⊥PD，又PD∩CD=D，满足定理所需条件；
（Ⅱ）以点A为坐标原点，以AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系A-xyz，根据
•
=0可知PC⊥AN，从而平面AMN的法向量为
，而平面PAB的法向量可为
，求出两平面的法相交的夹角即可求出平面AMN与PAB所成锐二面角的余弦值．
（Ⅱ）以点A为坐标原点，以AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系A-xyz，根据
| PC |
| AN |
| PC |
| AD |
解答：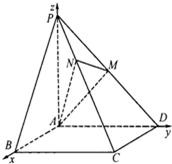
证明：（Ⅰ）因为四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，
则CD⊥侧面PAD
∴CD⊥AM，又PA=AD=2，∴AM⊥PD．
又PD∩CD=D，∴AM⊥平面PCD．（5分）
（Ⅱ）建立如图所示的空间直角坐标系A-xyz又PA=AD=2，
则有P（0，0，2），D（0，2，0）
M（0，1，1），C（2，2，0）
∴
=（2，2，-2）．
设N（x，y，z），∵
=
，则有
x-0=
(2-x)，∴x=
．
同理可得y=
，z=
．
即得N(
，
，
)．
由
•
=
+
-
=0，∴PC⊥AN
∴平面AMN的法向量为
=（2，2，-2），
而平面PAB的法向量可为
=（0，2，0），
∴cos＜
，
＞=
=
=
故所求平面AMN与PAB所成锐二面角的余弦值为
（13分）
证明：（Ⅰ）因为四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，则CD⊥侧面PAD
∴CD⊥AM，又PA=AD=2，∴AM⊥PD．
又PD∩CD=D，∴AM⊥平面PCD．（5分）
（Ⅱ）建立如图所示的空间直角坐标系A-xyz又PA=AD=2，
则有P（0，0，2），D（0，2，0）
M（0，1，1），C（2，2，0）
∴
| PC |
设N（x，y，z），∵
| PN |
| 1 |
| 2 |
| NC |
x-0=
| 1 |
| 2 |
| 2 |
| 3 |
同理可得y=
| 2 |
| 3 |
| 4 |
| 3 |
即得N(
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
由
| PC |
| AN |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴平面AMN的法向量为
| PC |
而平面PAB的法向量可为
| AD |
∴cos＜
| PC |
| AD |
| ||||
|
|
| 4 | ||||
|
| ||
| 3 |
故所求平面AMN与PAB所成锐二面角的余弦值为
| ||
| 3 |
点评：本小题主要考查直线与平面的位置关系、二面角及其平面角等有关知识，考查空间想象能力和思维能力，应用向量知识解决立体几何问题的能力．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图：已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，已知四棱锥P-ABCD的底面为菱形，∠BCD=60°，PD⊥AD．点E是BC边上的中点．
（2012•崇明县二模）如图，已知四棱锥P-ABCD的底面ABCD为正方形，PA⊥平面ABCD，E、F分别是BC，PC的中点，AB=2，AP=2．
（2012•吉林二模）如图，已知四棱锥P-ABCD的底面是正方形，PA⊥面ABCD，且PA=AD=2，点M，N分别在PD，PC上，