题目内容
【题目】已知椭圆 
+y2=1的左右焦点分别为F1 ， F2 ， 直线l过椭圆的右焦点F2与椭圆交于A，B 两点， （Ⅰ）当直线l的斜率为1，点P为椭圆上的动点，满足使得△ABP的面积为 
的点P有几个？并说明理由．
（Ⅱ）△ABF1的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时直线l的方程，若不存在，请说明理由．
【答案】解：（Ⅰ）由题意可知：椭圆 
+y2=1焦点在x轴上，右焦点F2（1，0）， 设直线l的方程为：y=x﹣1，则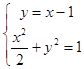 
，整理得：3x2﹣4x=0，
解得：x1=0，x2= 
，
则|AB|= 
|x1﹣x2|= 
，
设点P到直线l的距离为d，则S△ABP= 
|AB|d= × ×d= 
，
解得：d= 
，
设P（x0 ， y0），则P到直线l的距离d= 
，
令t=x0﹣y0﹣1，由 
，代入整理得：x02+2（x0﹣1﹣t）2=2，
化简整理得：3x02﹣4（1+t）x0+2t2+4t=0，
由△≥0，解得：﹣ 
﹣1≤t≤﹣ +1，
当﹣ ﹣1≤t＜0，椭圆上方的点到直线l的距离的最大值为 
＞ ，
则椭圆上存在两个这样的点P，使得△ABP的面积S△ABP= ，
当0≤t≤﹣ +1，椭圆下方的点到直线l的距离的最大值为 ＜ ，
则椭圆下方不存在这样的P点，使得△ABP的面积S△ABP= 
，
综上可知：椭圆上存在这样的P点有二个；
（Ⅱ）△ABF1的内切圆的半径为r， 
= （|AF1|+|BF1|+|AB|）×r= 4a×r，
∴要使内切圆的面积最大，即使得△ABF1最大，设直线l：x=my+1，
∴ 
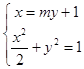，整理得：（m2+2）y2+2my﹣1=0…10分
由△=8（1+m2）＞0，
|y1﹣y2|= 
= 
，
设点F1到直线l的距离为h则： = |AB|×h= 
= ，
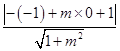令t= ，t≥0，则 = 
= 
≤ 
= ，
当且仅当t= 
，即m=0时， 取得最大值，
∴△ABF1面积最大值为 ，
则rmax= ，
∴△ABF1的内切圆的面积最大值为 
，此时直线l的方程为x=1
【解析】（Ⅰ）由椭圆 
+y2=1焦点在x轴上，右焦点F2（1，0），设直线l的方程为：y=x﹣1，代入椭圆方程，利用两点之间的距离公式，求得丨AB丨，根据三角形的面积公式求得点P到直线l的距离为d，利用点到直线的距离公式与d比较即可求得P点坐标；（Ⅱ）△ABF1的内切圆的半径为r， 
= 
4a×r，要使内切圆的面积最大，即使得△ABF1最大，将直线方程代入椭圆方程，利用韦达定理，点到直线的距离公式及基本不等式的性质，即可求得得△ABF1最大值，求得内切圆的半径及面积和直线l的方程．
