题目内容
【题目】某家具厂有方木料90 ![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 ![]() ,五合板2
,五合板2 ![]() ,生产每个书橱需要方木料0.2
,生产每个书橱需要方木料0.2![]() ,五合板1
,五合板1 ![]() ,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
【答案】生产书桌100张、书橱400个,可使所得利润最大.
【解析】
设生产书桌![]() 张,书橱
张,书橱![]() 个,利润总额为
个,利润总额为![]() 元,可得
元,可得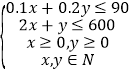 ,
,![]() ,利用线性规划可得结果.
,利用线性规划可得结果.
由题意可画表格如下:
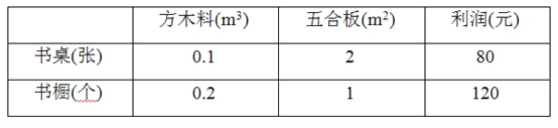
设生产书桌x张,书橱y个,利润总额为z元,
则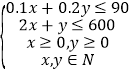 ,
,![]() .
.
在直角坐标平面内作出上面不等式组所表示的平面区域,即可行域.
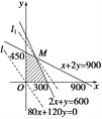
作直线![]() ,即直线
,即直线![]() .
.
把直线![]() 向右上方平移至
向右上方平移至![]() 的位置时,直线经过可行域上的点
的位置时,直线经过可行域上的点![]() ,
,
此时![]() 取得最大值.
取得最大值.
由![]()
解得点![]() 的坐标为
的坐标为![]() .
.
所以当![]() ,
,![]() 时,
时,![]() 的最大值为
的最大值为
![]() (元).
(元).
因此,生产书桌100张、书橱400个,可使所得利润最大.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
