题目内容
.(本小题满分14分)用数学归纳法证明:1+3+5+…+(2n-1)=n2(n∈N+).
证明:当n=1时,左边1=12=右边,结论成立;
当n=2时,左边1+3=22=右边,结论成立;
假设n=k时结论成立,即1+3+5+…+(2k-1)=k2;
当n=k+1时,左边=1+3+5+…+(2k-1)+[2(k+1)-1]= k2+[2(k+1)-1]= k2+2k+1=(k+1)2=右边
所以,原命题结论成立.
当n=2时,左边1+3=22=右边,结论成立;
假设n=k时结论成立,即1+3+5+…+(2k-1)=k2;
当n=k+1时,左边=1+3+5+…+(2k-1)+[2(k+1)-1]= k2+[2(k+1)-1]= k2+2k+1=(k+1)2=右边
所以,原命题结论成立.
略

练习册系列答案
相关题目
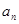 }满足
}满足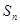 +
+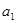 ,
,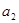 ,
,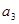 的值;
的值; 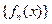 满足
满足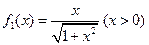 ,
,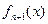 =
=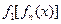 。
。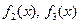 ;
;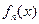 的解析式,并用数学归纳法证明。
的解析式,并用数学归纳法证明。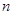 堆的第
堆的第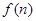 表示第
表示第


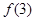 ;
;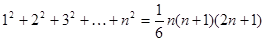 )
)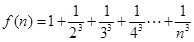 ,
,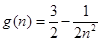 ,
,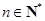 .
. 时,试比较
时,试比较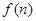 与
与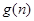 的大小关系;
的大小关系;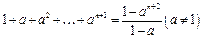 ,在验证
,在验证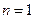 成立时,左边计算所得的项是
成立时,左边计算所得的项是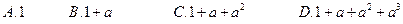
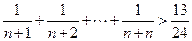 (
(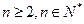 )的过程中,从“
)的过程中,从“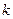 到
到 ”左端需增加的代数式为 ( )
”左端需增加的代数式为 ( )