题目内容
将数列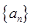 的各项按照第1行排
的各项按照第1行排 ,第2行自左至右排
,第2行自左至右排 ,第3行…的规律,排成如图所示的三角形形状.
,第3行…的规律,排成如图所示的三角形形状.
(Ⅰ)若数列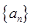 是首项为1,公差为3的等差数列,写出图中第五行第五个数;
是首项为1,公差为3的等差数列,写出图中第五行第五个数;
(Ⅱ)若函数 且
且 ,求数列
,求数列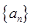 的通项公式;
的通项公式;
(Ⅲ)设 为图中第
为图中第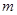 行所有项的和,在(Ⅱ)的条件下,用含
行所有项的和,在(Ⅱ)的条件下,用含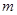 的代数式表示
的代数式表示 .
.
(Ⅰ)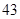 (Ⅱ)
(Ⅱ)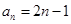 (
(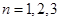 )(Ⅲ)
)(Ⅲ)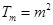
解析试题分析:(Ⅰ)因为数列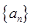 是首项为1,公差为3的等差数列,
是首项为1,公差为3的等差数列,
所以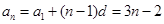 ,
,
因为图中前4行共有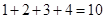 个数,
个数,
所以第五行第五个数是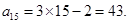 …2分
…2分
(Ⅱ)设数列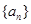 的前n项和为
的前n项和为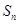 .
.
由 得,
得,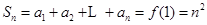 . …3分
. …3分
当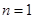 时,
时,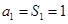 ;
;
当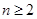 时,
时,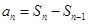
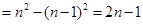 .
.
又当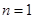 时,
时, ,
,
所以数列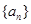 的通项公式为:
的通项公式为: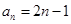 (
(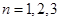 ). …6分
). …6分
(Ⅲ)图中前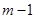 行共有项数为
行共有项数为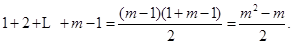 …8分
…8分
由(Ⅱ)知,数列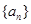 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列,
所以,图中第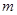 行第一个数为
行第一个数为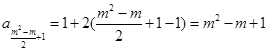 …10分
…10分
即,第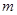 行的
行的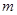 个数构成以
个数构成以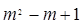 为首项,2为公差的等差数列,
为首项,2为公差的等差数列,
故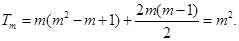 …12分
…12分
考点:本小题主要考查借助三角形形状图形研究等差数列的性质,等差数列的通项公式的求法,由数列的前n项和求数列的通项公式等,考查学生综合运用知识的能力和分析问题、解决问题的能力.
点评:由数列的前n项和求数列的通项公式时一定要注意讨论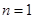 和
和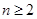 两种情况,不要把
两种情况,不要把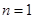 漏掉.数列的综合应用问题是高考重点考查的内容,同学们要加以重视.
漏掉.数列的综合应用问题是高考重点考查的内容,同学们要加以重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, ,且
,且
 .
. ,求
,求 是的通项公式;
是的通项公式; 是
是 与
与 的等差中项,求
的等差中项,求 的值,并证明:对任意的
的值,并证明:对任意的 ,
, 是
是 与
与 的等差中项.
的等差中项. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。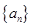 是等差数列,其前n项和公式为
是等差数列,其前n项和公式为 ,
,
 的值;
的值;  为等差数列,公差
为等差数列,公差 ,
, 是数列
是数列 项和, 且
项和, 且 .
. ;(2)令
;(2)令 ,求数列
,求数列 的前
的前 .
. 中,
中,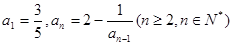 ,数列
,数列 满足
满足 .
. 中,
中, .
. ,且
,且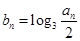 ,求数列
,求数列 的前
的前 项和
项和 .
. 中,
中, 是其前
是其前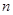 项和,
项和, ,求:
,求: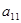 及
及 .
.