Question

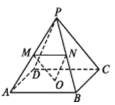
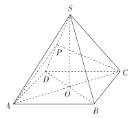
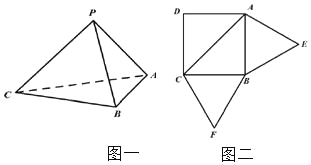
【题目】已知三棱锥（如图一）的平面展开图（如图二）中，四边形为边长等于的正方形，和均为正三角形，在三棱锥中：

（Ⅰ）证明：平面平面；

（Ⅱ）若点为棱上一点且，求二面角的余弦值．

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）.

【解析】

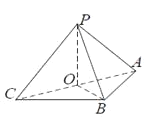
（Ⅰ）设的中点为，连接，，证明， ，平面，然后证明平面平面．

（Ⅱ）以，，所在直线分别为轴，轴，轴建立如图示空间直角坐标系，求出平面的法向量，平面的法向量，利用空间向量的数量积求解二面角的余弦值即可．

解：（Ⅰ）设的中点为，连接，．

由题意，得，， ．

在中，，为的中点， ，

在中，，，， ，

．

，，平面，平面，

平面，平面平面．

（Ⅱ）由平面，， ，，

于是以，，所在直线分别为轴，轴，轴建立如图示空间直角坐标系，

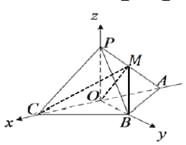
则， ， ， ，， ， ， ， ．

设平面的法向量为，

则由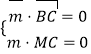得： ．令，得，，即．

设平面的法向量为，

由得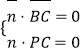： ，令，得，z＝1，即．

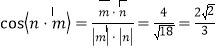．由图可知，二面角的余弦值为．