题目内容
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图（每个受访者都只能在问卷的5个活动中选择一个），以下结论错误的是（ ）
A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中，选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中，选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中，选择“公益广告”的人数比选择“学校要求”的少8个
【答案】D
【解析】
先对图表数据分析处理，再结合简单的合情推理逐一检验即可得解．
对于选项A，若回答该问卷的总人数不可能是100个，则选择③④⑤的同学人数不为整数，故A正确，
对于选项B，由统计图可知，选择“设置分类明确的垃圾桶”的人数最多，故B正确，
对于选项C，由统计图可知，选择“学校团委会宣传”的人数最少，故C正确，
对于选项D，由统计图可知，选择“公益广告”的人数比选择“学校要求”的少8%，故D错误，
故选：D．
智能训练练测考系列答案
【题目】“工资条里显红利，个税新政入民心”.随着2019年新年钟声的敲响，我国自1980年以来，力度最大的一次个人所得税（简称个税）改革迎来了全面实施的阶段.某
从业者为了解自己在个税新政下能享受多少税收红利，绘制了他在26岁-35岁（2009年-2018年）之间各年的月平均收入
（单位：千元）的散点图：(注：年龄代码1-10分别对应年龄26-35岁)
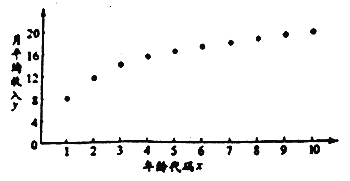
（1）由散点图知，可用回归模型
拟合与
的关系，试根据有关数据建立关于的回归方程；
（2）如果该从业者在个税新政下的专项附加扣除为3000元/月，试利用（1）的结果，将月平均收入视为月收入，根据新旧个税政策，估计他36岁时每个月少缴纳的个人所得税.
附注：①参考数据：
，
，
，
，
，
，
，其中
：取
，
.
②参考公式：回归方程
中斜率和截距的最小二乘估计分别为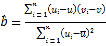
，
.
③新旧个税政策下每月应纳税所得额（含税）计算方法及税率表如下：
旧个税税率表（个税起征点3500元） | 新个税税率表（个税起征点5000元） | |||
缴税 级数 | 每月应纳税所得额（含税） | 税率 | 每月应纳税所得额（含税） | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
【题目】某手机厂商在销售200万台某型号手机时开展“手机碎屏险”活动.活动规则如下：用户购买该型号手机时可选购“手机碎屏险”，保费为
元.若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这200万台该型号手机全部销售完毕一年后，在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取1000名，每名用户赠送1000元的红包.为了合理确定保费的值，该手机厂商进行了问卷调查，统计后得到下表（其中
表示保费为元时愿意购买该“手机碎屏险”的用户比例）：
| 10 | 20 | 30 | 40 | 50 |
| 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
（1）根据上面的数据求出关于的回归直线方程；
（2）通过大数据分析，在使用该型号手机的用户中，购机后一年内发生碎屏的比例为
.已知更换一次该型号手机屏幕的费用为2000元，若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于70万元，能否把保费定为5元？
参考公式：回归方程
中斜率和截距的最小二乘估计分别为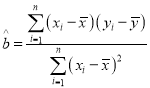
，
.
参考数据：表中的5个值从左到右分别记为
，
，
，
，
，相应的值分别记为
，
，
，
，
，经计算有
，其中
，
.
