题目内容
下列四个命题中,真命题的个数是( )
(1)如果a>0且a≠1,那么logaf(x)=logag(x)的充要条件是af(x)=ag(x)
(2)如果非零向量
,
,
满足:|
|=|
|=|
|,
+
=
,则
,
夹角为60°
(3)若直线a平行于平面α内的一条直线b,则a∥α
(4)无穷等比数列{an}的首项a1=
,公比q=
,设Tn=a12+a32+…+a2n-12,则
Tn=
.
(1)如果a>0且a≠1,那么logaf(x)=logag(x)的充要条件是af(x)=ag(x)
(2)如果非零向量
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
(3)若直线a平行于平面α内的一条直线b,则a∥α
(4)无穷等比数列{an}的首项a1=
| 1 |
| 2 |
| 1 |
| 2 |
| lim |
| n→+∞ |
| 1 |
| 3 |
分析:逐个判断:(1)注意对数的真数为正,故不能相互推出;(2)由向量的知识可求得夹角为120°;(3)由线面平行的判定定理可得;(4)为数列的极限问题,通过求和公式求到和,然后求极限可得结果.
解答:解:(1)由logaf(x)=logag(x)可推出af(x)=ag(x),但由af(x)=ag(x)不能推出logaf(x)=logag(x),
比如当f(x)=g(x)为负值时会使对数无意义,故为假命题;
(2)设向量
,
的夹角为θ,由
+
=
平方可得,|
|2+|
|2+2|
||
|cosθ=|
|2,
解得cosθ=-
,θ=120°,故为假命题;
(3)由线面平行的判定定理可知:平面外的直线a平行于平面α内的一条直线b,才有a∥α,故为假命题;
(4)无穷等比数列{an}的首项a1=
,公比q=
,
则Tn=a12+a32+…+a2n-12是首项为
,公比为
的等比数列的前n项和,
故Tn=a12+a32+…+a2n-12=
=
(1-
),可得
Tn=
,故为假命题.
故选A.
比如当f(x)=g(x)为负值时会使对数无意义,故为假命题;
(2)设向量
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
解得cosθ=-
| 1 |
| 2 |
(3)由线面平行的判定定理可知:平面外的直线a平行于平面α内的一条直线b,才有a∥α,故为假命题;
(4)无穷等比数列{an}的首项a1=
| 1 |
| 2 |
| 1 |
| 2 |
则Tn=a12+a32+…+a2n-12是首项为
| 1 |
| 4 |
| 1 |
| 16 |
故Tn=a12+a32+…+a2n-12=
| ||||
1-
|
| 4 |
| 15 |
| 1 |
| 16n |
| lim |
| n→+∞ |
| 4 |
| 15 |
故选A.
点评:本题为命题真假的判断,涉及向量,指数函数和对数函数,数列的极限等问题,属基础题.

练习册系列答案
相关题目
(如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是( )
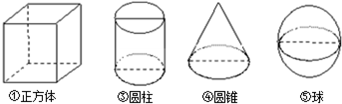

| A、①② | B、②③ | C、②④ | D、③④ |
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )