Question

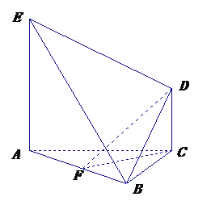
【题目】如图，已知平面，,是边长为2的等边三角形，为的中点，且；

(Ⅰ)求证：平面；

(Ⅱ)求证：平面平面；

(Ⅲ)求直线与平面所成角的正弦值.

Answer 1

【答案】（I）详见解析；（II）详见解析；（III）.

【解析】

（I）取中点，连，证明四边形为平行四边形，即可（II）可证平面即可（III）根据条件可知为直线与平面所成角，解三角形即可.

(Ⅰ)证明：取中点，连

为的中点， 且

又

且

四边形为平行四边形，

，又平面，平面

平面；

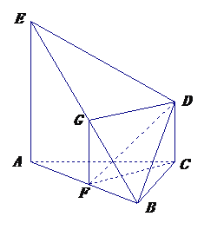
(Ⅱ)证明： 为的中点，是边长为2的等边三角形

平面,平面,

,又

平面, 平面

平面平面；

(Ⅲ) 平面,

平面,

为斜线在平面上的射影，

为直线与平面所成角,

在中，由条件易求得

即直线与平面所成角的正弦值为.