题目内容
解不等式

{x|x> }.
}.
 }.
}.分析:关键是去掉绝对值.
方法1:零点分段讨论法(利用绝对值的代数定义)
①当 时,
时, ∴
∴ ∴4<1
∴4<1
②当 时∴
时∴

 ,∴
,∴
③当 时∴
时∴
 -4<1
-4<1 ∴
∴
综上,原不等式的解集为
也可以这样写:
解:原不等式等价于① 或②
或② 或 ③
或 ③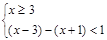 ,
,
解
①的解集为φ,
②的解集为{x| <x<3},
<x<3},
③的解集为{x|x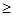 3},∴原不等式的解集为{x|x>
3},∴原不等式的解集为{x|x> }.
}.
方法2:数形结合:从形的方面考虑,不等式|x-3|-|x+1|<1表示数轴上到3和-1两点的距离之差小于1的点
∴原不等式的解集为{x|x> }.
}.
方法1:零点分段讨论法(利用绝对值的代数定义)
①当
 时,
时, ∴
∴ ∴4<1
∴4<1
②当
 时∴
时∴

 ,∴
,∴
③当
 时∴
时∴
 -4<1
-4<1 ∴
∴
综上,原不等式的解集为

也可以这样写:
解:原不等式等价于①
 或②
或② 或 ③
或 ③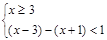 ,
,解
①的解集为φ,
②的解集为{x|
 <x<3},
<x<3},③的解集为{x|x
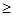 3},∴原不等式的解集为{x|x>
3},∴原不等式的解集为{x|x> }.
}.方法2:数形结合:从形的方面考虑,不等式|x-3|-|x+1|<1表示数轴上到3和-1两点的距离之差小于1的点

∴原不等式的解集为{x|x>
 }.
}.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤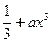 ;
; ≤1,
≤1, ,求证:
,求证: ≤
≤

 ,则
,则

 满足
满足 ,则
,则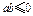

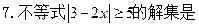 ( )
( )



 的解集为__________________
的解集为__________________