题目内容
选修4—5;不等式选讲
已知a,b,c,d都是实数,且a2+b2=1,c2+d2=1,求证:|ac+bd|≤1.
已知a,b,c,d都是实数,且a2+b2=1,c2+d2=1,求证:|ac+bd|≤1.
略
设a=cos ,b=sin
,b=sin ,c=cos
,c=cos ,d=sin
,d=sin
|a c+bd|=|
c+bd|=| cos
cos cos
cos +sin
+sin sin
sin |
|
=|cos( -
- )|≤1
)|≤1
方法二:只需证(ac+bd)2≤(a2+b2)(c2+d2)
即证:2abcd≤a2d2+b2c2
即证:(ad-bc)2≥0
上式显然成立
∴原不等式成立。
 ,b=sin
,b=sin ,c=cos
,c=cos ,d=sin
,d=sin
|a
 c+bd|=|
c+bd|=| cos
cos cos
cos +sin
+sin sin
sin |
| =|cos(
 -
- )|≤1
)|≤1 方法二:只需证(ac+bd)2≤(a2+b2)(c2+d2)
即证:2abcd≤a2d2+b2c2
即证:(ad-bc)2≥0
上式显然成立
∴原不等式成立。

练习册系列答案
相关题目

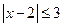 的解集为( )
的解集为( )



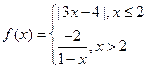 则不等式
则不等式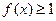 的解集是
的解集是



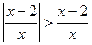 的解集是
的解集是



 的解集为 .
的解集为 . 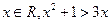 ”的否定是“任意
”的否定是“任意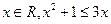 ”;
”;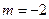 ”是“直线
”是“直线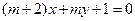 与直线
与直线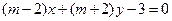 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;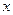 的不等式
的不等式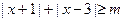 的解集为
的解集为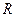 ,则
,则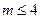 .
.