题目内容
1)设 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤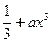 ;
;
(2)设 ≤1,
≤1, ,求证:
,求证: ≤
≤
 ≤1,求一个正常数a,使得x≤
≤1,求一个正常数a,使得x≤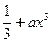 ;
;(2)设
 ≤1,
≤1, ,求证:
,求证: ≤
≤
(1)同解析,(2)同解析。
⑴ x≤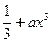 可化为
可化为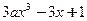 ≥0,令
≥0,令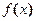 =
=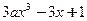 ,
,
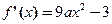 ,由
,由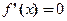 得,
得,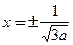
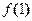 =3a-2≥0,
=3a-2≥0,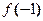 =-3a+4≥0,∴
=-3a+4≥0,∴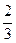 ≤
≤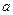 ≤
≤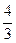 , ①
, ①
∴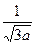 ∈[-1,1],
∈[-1,1],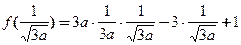 ≥0,即
≥0,即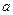 ≥
≥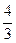 ②
②
由①、②得,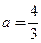 .
.
从而当 ≤1时,
≤1时,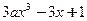 =
=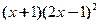 ≥0,即x≤
≥0,即x≤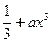 .
.
⑵ 由⑴知,对 ≤1,有
≤1,有 ≤
≤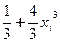 ,(i=1,2,…,n)
,(i=1,2,…,n)
将这n个式子求和,得 ≤
≤ .
.
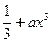 可化为
可化为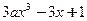 ≥0,令
≥0,令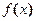 =
=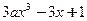 ,
,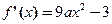 ,由
,由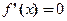 得,
得,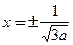
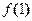 =3a-2≥0,
=3a-2≥0,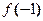 =-3a+4≥0,∴
=-3a+4≥0,∴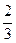 ≤
≤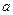 ≤
≤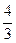 , ①
, ①∴
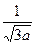 ∈[-1,1],
∈[-1,1],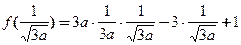 ≥0,即
≥0,即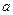 ≥
≥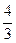 ②
②由①、②得,
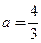 .
. 从而当
 ≤1时,
≤1时,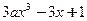 =
=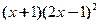 ≥0,即x≤
≥0,即x≤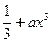 .
. ⑵ 由⑴知,对
 ≤1,有
≤1,有 ≤
≤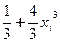 ,(i=1,2,…,n)
,(i=1,2,…,n)将这n个式子求和,得
 ≤
≤ .
. 
练习册系列答案
相关题目

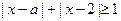 对任意实数
对任意实数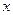 均成立,求实数
均成立,求实数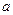 的取值范围
的取值范围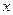 的不等式
的不等式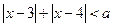 的解集不是空集,求参数
的解集不是空集,求参数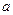 的取值范围。
的取值范围。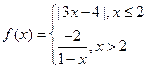 则不等式
则不等式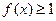 的解集是
的解集是



 的解集为 .
的解集为 . 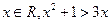 ”的否定是“任意
”的否定是“任意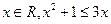 ”;
”;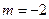 ”是“直线
”是“直线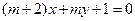 与直线
与直线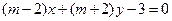 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;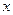 的不等式
的不等式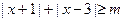 的解集为
的解集为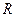 ,则
,则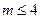 .
.