题目内容
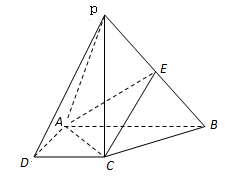
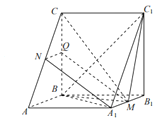
【题目】如图,在三棱柱ABC-A1B1C1中,侧面B1BCC1是正方形,M,N分别是A1B1,AC的中点,AB⊥平面BCM.
(Ⅰ)求证:平面B1BCC1⊥平面A1ABB1;
(Ⅱ)求证:A1N∥平面BCM;
(Ⅲ)若三棱柱ABC-A1B1C1的体积为10,求棱锥C1-BB1M的体积.

【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)![]()
【解析】
(Ⅰ)推导出AB⊥BC,BB1⊥BC,从而BC⊥平面A1ABB1,由此能证明平面B1BCC1⊥平面A1ABB1.
(Ⅱ)设BC中点为Q,连结NQ,MQ,推导出四边形A1MQN是平行四边形,从而A1N∥MQ,由此能证明A1N∥平面BCM.
(Ⅲ)连结A1B,根据棱柱和棱锥的体积公式,三棱锥B﹣A1B1C1的体积![]() ,棱锥C1﹣BB1M的体积
,棱锥C1﹣BB1M的体积![]() ,由此能求出结果.
,由此能求出结果.
证明:(Ⅰ)∵AB⊥平面BCM,BC平面BCM,∴AB⊥BC,
∵正方形B1BCC1,∴BB1⊥BC,
∵AB∩BB1=B,∴BC⊥平面A1ABB1,
∵BC平面B1BCC1,∴平面B1BCC1⊥平面A1ABB1;
(Ⅱ)设BC中点为Q,连结NQ,MQ,
∵M,N分别是A1B1,AC的中点,∴NQ∥AB,且NQ=![]() AB,
AB,
∵AB∥A1B1,且AB=A1B1,∴NQ∥A1M,且NQ=A1M,
∴四边形A1MQN是平行四边形,∴A1N∥MQ,
∵MQ平面BCM,A1N
∴A1N∥平面BCM.
(Ⅲ)连结A1B,根据棱柱和棱锥的体积公式,
得到三棱锥B-A1B1C1的体积![]() =
=![]() =
=![]() ,
,
∵M为A1B1的中点,
∴棱锥C1-BB1M的体积![]() =
=![]() =
=![]() =
=![]() .
.

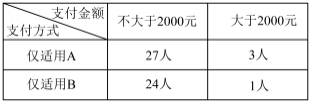
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的50名学生中有40人比较细心,另外10人比较粗心;在数学成绩不及格的50名学生中有20人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表:
列联表:
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 40 | ||
比较粗心 | |||
合计 | 50 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.