题目内容
设椭圆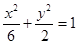
和双曲线
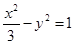有公共焦点为
、
，
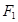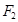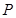是两曲线的一个公共点，则
∠
（ ）
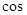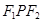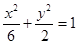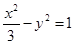和双曲线有公共焦点为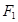、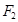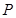，是两曲线的一个公共点，则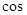∠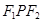（ ）A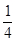． | B． | C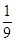． | D． |
B
不妨
。根据椭圆和双曲线定义得：
。
得
得
。
故选B
。根据椭圆和双曲线定义得：。得得。故选B
练习册系列答案
相关题目
题目内容
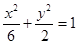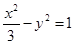和双曲线有公共焦点为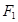、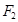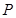，是两曲线的一个公共点，则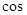∠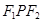（ ）| A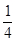． | B． | C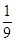． | D． |
。根据椭圆和双曲线定义得：。得得。
的椭圆
过点M（2，1），O为坐标原点，平行于OM的直线
交椭圆C于不同的两点A、B。
面积的最大值；
长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于
轴上方，
． 
，求点M的坐标；
的最小值．
的焦点坐标为
，长轴等于焦距的2倍．
的边
在
轴上，点
、
落在椭圆
及定点
，点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
与曲线C交于A、B两点，O是坐标原点，设
是否存在这样的直线
,它的离心率为
.直线
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
是椭圆C：
与圆F：
的一个交点，且圆心F是椭圆的一个焦点，（1）求椭圆C的方程；（2）过F的直线交圆与P、Q两点，连AP、AQ分别交椭圆与M、N点，试问直线MN是否过定点？若过定点，则求出定点坐标；若不过定点，请说明理由．
（m＞n＞0）和双曲线
（a＞b＞0）有相同的焦点F1，F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是 （ ）
