ЬтФПФкШн
ЁОЬтФПЁПдкЗЂЩњФГЙЋЙВЮРЩњЪТМўЦкМфЃЌгазЈвЕЛњЙЙШЯЮЊИУЪТМўдквЛЖЮЪБМфФкУЛгаЗЂЩњДѓЙцФЃШКЬхИаШОЕФБъжОЪЧЁАСЌај10ШеЃЌУПЬьаТдівЩЫЦВЁР§ВЛГЌЙ§7ШЫЁБ.вбжЊЙ§ШЅ10ШеЃЌ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕиаТдівЩЫЦВЁР§Ъ§ОнаХЯЂШчЯТЃК
Ш§ЕиаТдівЩЫЦВЁР§Ъ§ОнаХЯЂШчЯТЃК
![]() ЕиЃКзмЬхЦНОљЪ§ЮЊ3ЃЌжаЮЛЪ§ЮЊ4ЃЛ
ЕиЃКзмЬхЦНОљЪ§ЮЊ3ЃЌжаЮЛЪ§ЮЊ4ЃЛ
![]() ЕиЃКзмЬхЦНОљЪ§ЮЊ2ЃЌзмЬхЗНВюЮЊ3ЃЛ
ЕиЃКзмЬхЦНОљЪ§ЮЊ2ЃЌзмЬхЗНВюЮЊ3ЃЛ
![]() ЕиЃКзмЬхЦНОљЪ§ЮЊ1ЃЌзмЬхЗНВюДѓгк0ЃЛ
ЕиЃКзмЬхЦНОљЪ§ЮЊ1ЃЌзмЬхЗНВюДѓгк0ЃЛ
дђ![]() ЁЂ
ЁЂ![]() ЁЂ
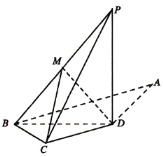
ЁЂ![]() Ш§ЕижаЃЌвЛЖЈУЛгаЗЂЩњДѓЙцФЃШКЬхИаШОЕФЪЧ__________Еи.
Ш§ЕижаЃЌвЛЖЈУЛгаЗЂЩњДѓЙцФЃШКЬхИаШОЕФЪЧ__________Еи.
ЁОД№АИЁП![]()
ЁОНтЮіЁП
ИљОнЦНОљЪ§ЃЌжаЮЛЪ§КЭЗНВюЕФЖЈвхМАаджЪЃЌвРДЮХаЖЯМДПЩ.
![]() ЕиЃЌЦНОљЪ§КЭжаЮЛЪ§ВЛФмЯожЦФГвЛЬьЕФ¨ЧÍɧ
ЕиЃЌЦНОљЪ§КЭжаЮЛЪ§ВЛФмЯожЦФГвЛЬьЕФ¨ЧÍɧ![]() ШЫЃЌЙЪВЛЪЧ
ШЫЃЌЙЪВЛЪЧ![]() Еи.
Еи.
![]() ЕиЃЌЕБзмЬхЦНОљЪ§ЮЊ2ЃЌ
ЕиЃЌЕБзмЬхЦНОљЪ§ЮЊ2ЃЌ
ИљОнЗНВюЙЋЪН![]()
МйЩшДцдкФГЬьаТдівЩЫЦ¨ЧÍɧ![]() ШЫЃЌЩшЮЊ
ШЫЃЌЩшЮЊ![]() ШЫЃЌ
ШЫЃЌ
дђ![]() ЃЌ
ЃЌ
![]() ВЛГЩСЂЃЌЙЪвЛЖЈУЛгаЗЂЩњДѓЙцФЃШКЬхИаШОЕФЪЧ
ВЛГЩСЂЃЌЙЪвЛЖЈУЛгаЗЂЩњДѓЙцФЃШКЬхИаШОЕФЪЧ![]() Еи.
Еи.
![]() ЕиЃЌЕБзмЬхЗНВюДѓгк0ЪБЃЌВЛжЊЕРзмЬхЗНВюЕФОпЬхЪ§жЕЃЌ
ЕиЃЌЕБзмЬхЗНВюДѓгк0ЪБЃЌВЛжЊЕРзмЬхЗНВюЕФОпЬхЪ§жЕЃЌ
УПЬьаТдівЩЫЦВЁР§ПЩвдГЌЙ§![]() ШЫЃЌЙЪВЛЪЧ
ШЫЃЌЙЪВЛЪЧ![]() Еи.
Еи.
ЙЪД№АИЮЊЃК![]()

 ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИ
ЕМбЇНЬГЬИпжааТПЮБъЯЕСаД№АИЁОЬтФПЁПФГзмЙЋЫОдкAЃЌBСНЕиЗжБ№гаМзЁЂввСНИіЯТЪєЙЋЫОЭЌжжаТФмдДВњЦЗЃЈетСНИіЙЋЫОУПЬьЖМЙЬЖЈЩњВњ50МўВњЦЗЃЉЃЌЫљЩњВњЕФВњЦЗОљдкБОЕиЯњЪл.ВњЦЗНјШЫЪаГЁжЎЧАашвЊЖдВњЦЗНјааадФмМьВтЃЌЕУЗжЕЭгк80ЗжЕФЖЈЮЊДЮЦЗЃЌашвЊЗЕГЇдйМгЙЄЃЛЕУЗжВЛЕЭгк80ЗжЕФЖЈЮЊе§ЦЗЃЌПЩвдНјШЫЪаГЁ.МьВтдБЭГМЦСЫМзЁЂввСНИіЯТЪєЙЋЫО100ЬьЕФЩњВњЧщПіМАУПМўВњЦЗгЏРћПїЫ№ЧщПіЃЌЪ§ОнШчБэЫљЪОЃК
Бэ1
МзЙЋЫО | ЕУЗж | [50ЃЌ60ЃЉ | [60ЃЌ70ЃЉ | [70ЃЌ80ЃЉ | [80ЃЌ90ЃЉ | [90ЃЌ100] |
МўЪ§ | 10 | 10 | 40 | 40 | 50 | |
ЬьЪ§ | 10 | 10 | 10 | 10 | 80 |
Бэ2
МзЙЋЫО | ЕУЗж | [50ЃЌ60ЃЉ | [60ЃЌ70ЃЉ | [70ЃЌ80ЃЉ | [80ЃЌ90ЃЉ | [90ЃЌ100] |
МўЪ§ | 10 | 5 | 40 | 45 | 50 | |
ЬьЪ§ | 20 | 10 | 20 | 10 | 70 |
Бэ3
УПМўе§ЦЗ | УПМўДЮЦЗ | |
МзЙЋЫО | гЏ2ЭђдЊ | Пї3ЭђдЊ |
ввЙЋЫО | гЏ3ЭђдЊ | Пї3.5ЭђдЊ |
ЃЈ1ЃЉЗжБ№ЧѓМзЁЂввСНИіЙЋЫОет100ЬьЩњВњЕФВњЦЗЕФе§ЦЗТЪЃЈгУАйЗжЪ§БэЪОЃЉ.
ЃЈ2ЃЉЪдЮЪМзЁЂввСНИіЙЋЫОет100ЬьЩњВњЕФВњЦЗЕФзмРћШѓФФИіИќДѓЃПЫЕУїРэгЩ.
ЃЈ3ЃЉШєвдМзЙЋЫОет100ЬьжаУПЬьВњЦЗРћШѓзмКЭЖдгІЕФЦЕТЪзїЮЊИХТЪЃЌДгМзЙЋЫОет100ЬьЫцЛњГщШЁ1ЬьЃЌМЧетЬьВњЦЗРћШѓзмКЭЮЊXЃЌЧѓXЕФЗжВМСаМАЦфЪ§бЇЦкЭћ.