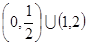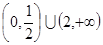题目内容
对于函数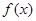 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为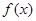 的不动点,已知函数
的不动点,已知函数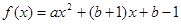 (a≠0).
(a≠0).
(1)当 时,求函数
时,求函数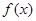 的不动点;
的不动点;
(2)若对任意实数b,函数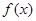 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
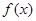 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为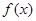 的不动点,已知函数
的不动点,已知函数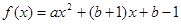 (a≠0).
(a≠0).(1)当
 时,求函数
时,求函数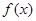 的不动点;
的不动点;(2)若对任意实数b,函数
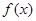 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;(1) 1为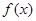 的不动点(2)
的不动点(2) 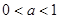
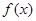 的不动点(2)
的不动点(2) 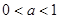
试题分析:解:(1)由题得:
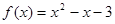 ,因为
,因为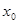 为不动点,
为不动点,因此有
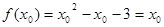 ,即
,即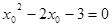 2分
2分所以
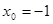 或
或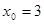 ,即3和-1为
,即3和-1为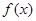 的不动点。 5分
的不动点。 5分(2)因为
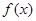 恒有两个不动点,
恒有两个不动点,∴
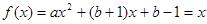 ,
,即
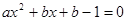 (※)恒有两个不等实数根, 8分
(※)恒有两个不等实数根, 8分由题设
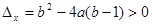 恒成立, 10分
恒成立, 10分即对于任意b∈R,有
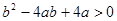 恒成立,
恒成立,所以有
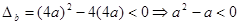 , 12分
, 12分∴
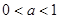 13分
13分点评:解题的关键是对新定义的理解,建立方程,将不动点的问题,转化为结合一元二次方程中必然有两个不等的实数根来求解参数的取值范围。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
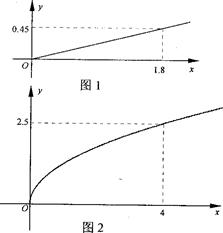
 小时的收费为
小时的收费为 元
元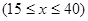 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动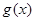 元
元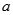 和
和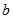 ,定义运算“
,定义运算“ ”:
”: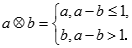 设函数
设函数 ,
,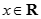 ,若函数
,若函数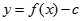 的图像与
的图像与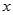 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数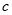 的取值范围是( )
的取值范围是( ) 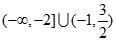
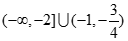
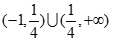
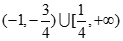
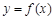 在区间
在区间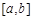 上是减函数,则
上是减函数,则 上是
上是

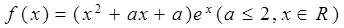
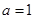 ,求函数
,求函数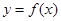 在点(0,
在点(0,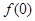 )处的切线方程;
)处的切线方程;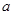 ,使得
,使得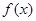 的极大值为3.若存在,求出
的极大值为3.若存在,求出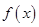 在定义域
在定义域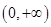 上为增函数,且满足
上为增函数,且满足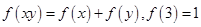
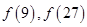 的值 (2)解不等式
的值 (2)解不等式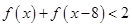
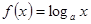 ,在
,在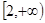 上恒有
上恒有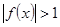 ,则实数
,则实数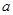 的范围是( )
的范围是( )