题目内容
(本小题满分14分)
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知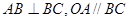 且
且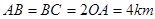 ,曲线段
,曲线段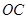 是以点
是以点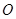 为顶点且开口向右的抛物线的一段.
为顶点且开口向右的抛物线的一段.
(I)建立适当的坐标系,求曲线段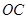 的方程;
的方程;
(II)如果要使矩形的相邻两边分别落在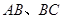 上,且一个顶点
上,且一个顶点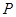 落在曲线段
落在曲线段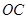 上,问如何规划才能使矩形工业园区的用地面积最大?并求这个最大值.
上,问如何规划才能使矩形工业园区的用地面积最大?并求这个最大值.

【答案】
(I) 以O为原点,OA所在直线为y轴建立直角坐标系(如图),
依题可设抛物线方程为y2=2px(p>0),且C(4,2).由此可得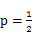 ,
,
故曲线段OC的方程为y2=x(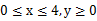 ).……………………………6分
).……………………………6分
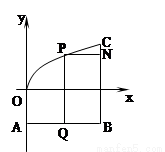 (II) 设P(t2,t)(
(II) 设P(t2,t)(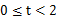 ),
),
则在矩形PQBN中,|PQ|=2+t,|PN|=4-t2.
工业园区面积S(t)=|PQ||PN|=(2+t)( 4-t2)= -t3-2t2+4t+8.
……………………………8分
导数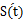 = -3t2-4t+4,
= -3t2-4t+4,
当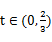 时,
时,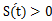 ; 当
; 当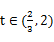 时,
时,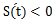 .
.
所以S(t)在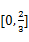 上为增函数,在
上为增函数,在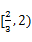 上为减函数…………10分.
上为减函数…………10分.
所以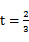 时,Smax=
时,Smax=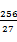 ;此时
;此时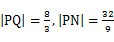 .…………13分
.…………13分
答:当矩形的长为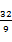 km,宽为
km,宽为 km时,园区面积最大,最大值为
km时,园区面积最大,最大值为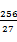 km2.-----14分
km2.-----14分
【解析】略

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)