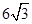题目内容
在平面直角坐标系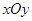 中,设点
中,设点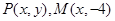 ,坐标原点
,坐标原点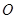 在以线段
在以线段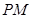 为直径的圆上
为直径的圆上
(Ⅰ)求动点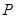 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)过点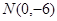 的直线
的直线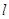 与轨迹C交于两点
与轨迹C交于两点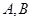 ,点
,点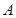 关于
关于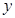 轴的对称点为
轴的对称点为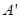 ,试判断直线
,试判断直线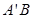 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
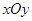 中,设点
中,设点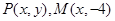 ,坐标原点
,坐标原点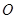 在以线段
在以线段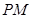 为直径的圆上
为直径的圆上(Ⅰ)求动点
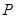 的轨迹C的方程;
的轨迹C的方程;(Ⅱ)过点
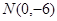 的直线
的直线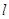 与轨迹C交于两点
与轨迹C交于两点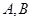 ,点
,点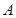 关于
关于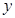 轴的对称点为
轴的对称点为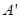 ,试判断直线
,试判断直线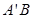 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.(I)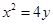 (II)
(II)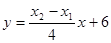 所以,直线
所以,直线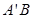 恒过定点
恒过定点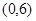
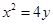 (II)
(II)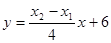 所以,直线
所以,直线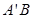 恒过定点
恒过定点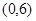
(Ⅰ)利用垂直关系列出关系式,然后化简即可;(Ⅱ)联立方程求出中点坐标,然后利用直线恒过定点问题解决
(I)由题意可得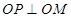 , ……………1分
, ……………1分
所以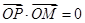 ,即
,即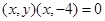
即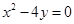 ,即动点
,即动点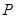 的轨迹C的方程为
的轨迹C的方程为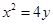 ……4分
……4分
(II)设直线 的方程为
的方程为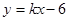 ,
,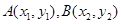 ,则
,则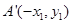 .
.
由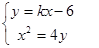 消
消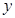 整理得
整理得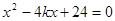 ,则
,则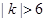 ,
,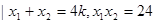 直线
直线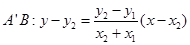
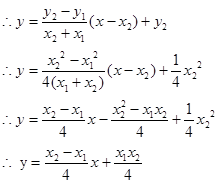
即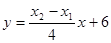 所以,直线
所以,直线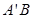 恒过定点
恒过定点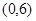
(I)由题意可得
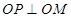 , ……………1分
, ……………1分所以
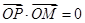 ,即
,即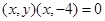
即
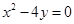 ,即动点
,即动点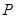 的轨迹C的方程为
的轨迹C的方程为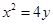 ……4分
……4分(II)设直线
 的方程为
的方程为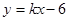 ,
,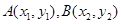 ,则
,则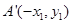 .
.由
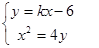 消
消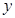 整理得
整理得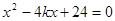 ,则
,则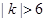 ,
,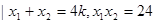 直线
直线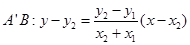
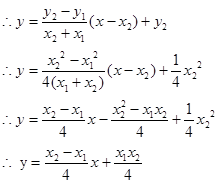
即
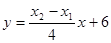 所以,直线
所以,直线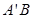 恒过定点
恒过定点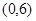

练习册系列答案
相关题目
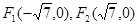 离心率e=
离心率e=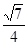 (1)求椭圆的方程。(2)若CD为过左焦点
(1)求椭圆的方程。(2)若CD为过左焦点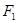 的弦,求
的弦,求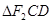 的周长
的周长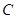 的中心在原点,一个焦点
的中心在原点,一个焦点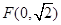 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是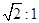 .若椭圆
.若椭圆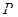 的横坐标为1,过点
的横坐标为1,过点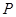 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线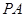 ,
,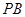 分别交椭圆
分别交椭圆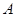 ,
,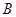 .
.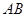 的斜率为定值;
的斜率为定值;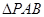 面积的最大值.
面积的最大值.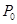 沿与AB夹角为
沿与AB夹角为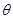 的方向射到BC上的点
的方向射到BC上的点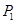 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点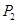 、
、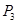 和
和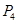 (入射角等于反射角),设
(入射角等于反射角),设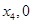 ),若
),若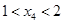 ,则tan
,则tan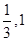 ) B.(
) B.(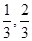 ) C.(
) C.(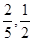 ) D.(
) D.(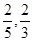 )
)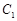 是以
是以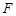 为焦点的抛物线
为焦点的抛物线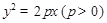 ,
,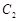 是以直线
是以直线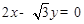 与
与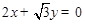 为渐近线,以
为渐近线,以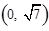 为一个焦点的双曲线.
为一个焦点的双曲线.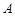 和
和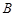 ,求
,求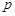 的取值范围,并求
的取值范围,并求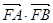 的最大值;
的最大值;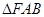 的面积
的面积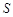 满足
满足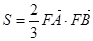 ,求
,求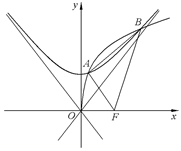
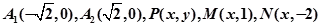 ,若实数
,若实数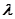 使得
使得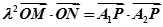 (
(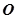 为坐标原点)
为坐标原点)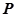 点的轨迹方程,并讨论
点的轨迹方程,并讨论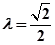 时,若过点
时,若过点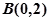 的直线与(1)中
的直线与(1)中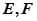 (
(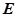 在
在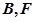 之间),试求
之间),试求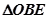 与
与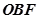 面积之比的取值范围。
面积之比的取值范围。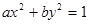 与直线
与直线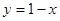 交于
交于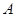
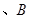 两点,过原点与线段
两点,过原点与线段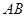 中点的直线的斜率为
中点的直线的斜率为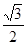 ,则
,则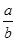 的值为 ( )
的值为 ( )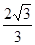
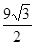
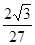
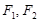 分别是双曲线
分别是双曲线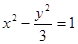 的左、右焦点,
的左、右焦点,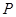 是双曲线上一点,且满足
是双曲线上一点,且满足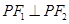 ,则
,则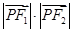 的值是( )
的值是( )