题目内容
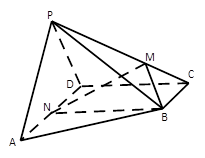
(本题满分10分)如图,已知四棱锥 底面
底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 、
、 的中点.
的中点.
(1)证明:
(2)设 , 若
, 若 为线段
为线段 上的动点,
上的动点, 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为
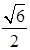 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.
 底面
底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 、
、 的中点.
的中点. (1)证明:

(2)设
 , 若
, 若 为线段
为线段 上的动点,
上的动点, 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为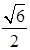 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.
.(1)证明:见解析;(2)异面直线所成角300
试题分析:(I)根据题意可得:△ABC为正三角形,所以AE⊥BC,又因为BC∥AD,所以AE⊥AD.又PA⊥AE,且PA∩AD=A,所以AE⊥平面PAD,进而可得答案;
(Ⅱ)先根据条件由(1)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角. 在Rt△EAH中,AE=
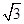 ,所以 当AH最短时,∠EHA最大进而得到异面直线的所成的角。
,所以 当AH最短时,∠EHA最大进而得到异面直线的所成的角。(1)证明:由四边形ABCD为菱形,∠ABC=60°,
可得△ABC为正三角形.因为E为BC的中点,
所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,
AE
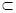 平面ABCD,所以PA⊥AE.而 PA
平面ABCD,所以PA⊥AE.而 PA 平面PAD,
平面PAD,AD
 平面PAD 且PA∩AD=A,所以 AE⊥平面PAD,
平面PAD 且PA∩AD=A,所以 AE⊥平面PAD,又PD
 平面PAD.所以 AE⊥PD.
平面PAD.所以 AE⊥PD. (2)解:设AB=2,H为PD上任意一点,
连接AH,EH. 由(1)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=
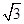 ,所以 当AH最短时,∠EHA最大,
,所以 当AH最短时,∠EHA最大,即当AH⊥PD时,∠EHA最大.此时tan∠EHA=
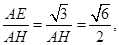
因此AH=
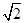 .又AD=2,所以∠ADH=45所以 PA=2.
.又AD=2,所以∠ADH=45所以 PA=2.异面直线所成角300
点评:解决此类问题的关键是熟练掌握几何体的结构特征,以便利用已知条件得到空间的线面关系,并且便于建立坐标系利用向量的有关运算解决空间角等问题

练习册系列答案
相关题目
 的侧面
的侧面 是等边三角形,
是等边三角形,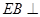 平面
平面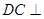 平面
平面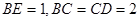 ,
, 是棱
是棱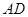 的中点.
的中点.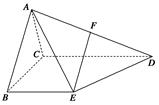
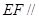 平面
平面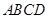 满足
满足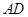 ∥
∥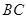 ,
,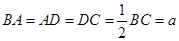 ,
,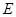 是
是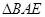 沿着
沿着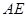 翻折成
翻折成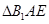 ,使面
,使面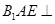 面
面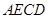 ,
,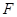 为
为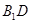 的中点.
的中点. 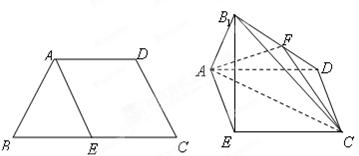
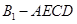 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: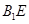 ∥面
∥面 ;
;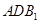 与面
与面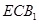 所成二面角的余弦值.
所成二面角的余弦值.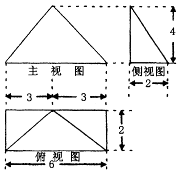
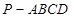 的侧面
的侧面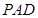 垂直于底面
垂直于底面 ,
,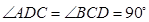
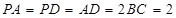 ,
,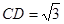 ,
,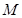 在棱
在棱 上,
上, 是
是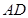 的中点,二面角
的中点,二面角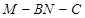 为
为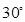 求
求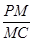 的值;
的值;