题目内容
(本小题满分14分)
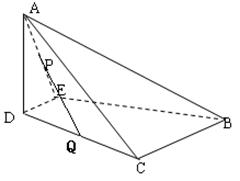
如图,沿等腰直角三角形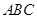 的中位线
的中位线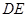 ,将平面
,将平面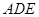 折起,平面
折起,平面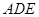 ⊥平面
⊥平面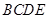 ,得到四棱锥
,得到四棱锥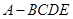 ,
,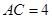 ,设
,设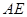 、
、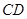 的中点分别为
的中点分别为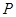 、
、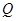 ,
,
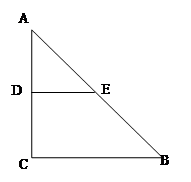
(1)求证:平面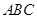 ⊥平面
⊥平面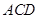
(2)求证:
(3)求平面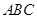 与平面
与平面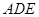 所成锐二面角的余弦值。
所成锐二面角的余弦值。
如图,沿等腰直角三角形
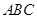 的中位线
的中位线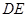 ,将平面
,将平面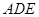 折起,平面
折起,平面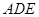 ⊥平面
⊥平面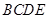 ,得到四棱锥
,得到四棱锥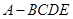 ,
,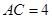 ,设
,设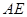 、
、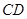 的中点分别为
的中点分别为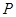 、
、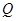 ,
,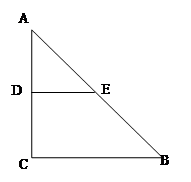

(1)求证:平面
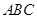 ⊥平面
⊥平面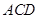
(2)求证:

(3)求平面
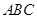 与平面
与平面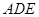 所成锐二面角的余弦值。
所成锐二面角的余弦值。(1)见解析(2)见解析(3)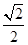
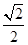
试题分析:(1)证明:
 平面
平面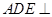 平面
平面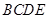 ,交线为
,交线为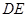 ,
, 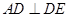 ,
, 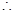
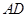
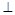 平面
平面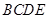 .
.
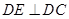 ,
, 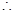
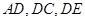 两两互相垂直,
两两互相垂直,以
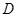 为原点建立空间直角坐标系, ……2分
为原点建立空间直角坐标系, ……2分因为
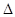
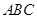 为等腰直角三角形,且
为等腰直角三角形,且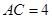 ,则
,则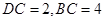 ,
,则
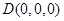 ,
,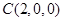 ,
,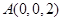 ,
,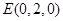 ,
,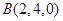 .
.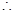
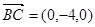 ,
,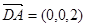 ,
,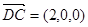 ,
,
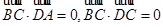 ,
,
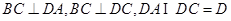 ,
,
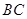
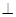 平面
平面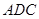 ,又
,又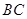
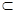 平面
平面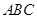
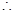 平面
平面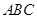 ⊥平面
⊥平面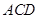 . ……5分
. ……5分(2)
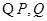 分别为
分别为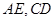 的中点,
的中点,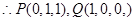 ,
,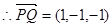 .
.设平面
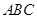 的法向量
的法向量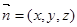 ,由于
,由于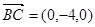
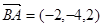
则
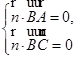 即
即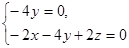 ,
,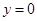 ,令
,令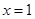 ,则
,则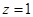 ,
, 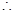
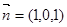 .
.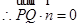 , 即
, 即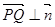
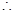
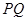 //平面
//平面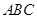 . ……9分
. ……9分(3)由(2)可知平面
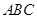 的法向量
的法向量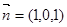 ,由于平面
,由于平面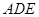 的法向量为
的法向量为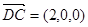 ,
,设平面
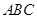 与平面
与平面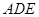 所成锐二面角为
所成锐二面角为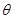 ,则
,则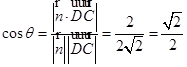 . ……14分
. ……14分点评:求二面角最常用的方法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,如果题目中没有说明,则要注意结合实际图形判断所求角是锐角还是钝角.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
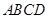 满足
满足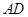 ∥
∥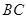 ,
,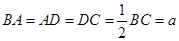 ,
,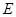 是
是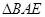 沿着
沿着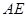 翻折成
翻折成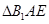 ,使面
,使面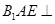 面
面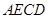 ,
,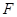 为
为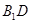 的中点.
的中点. 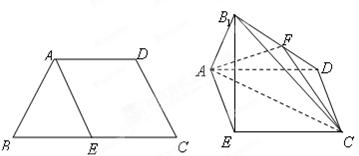
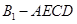 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: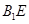 ∥面
∥面 ;
;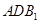 与面
与面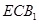 所成二面角的余弦值.
所成二面角的余弦值.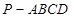 的侧面
的侧面 垂直于底面
垂直于底面 ,
,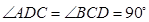
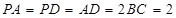 ,
,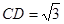 ,
,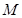 在棱
在棱 上,
上,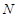 是
是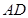 的中点,二面角
的中点,二面角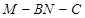 为
为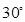 求
求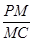 的值;
的值;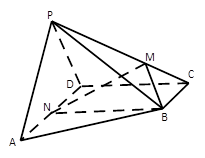
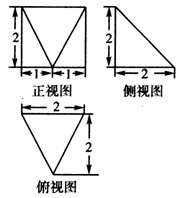





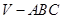 中,
中,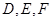 分别是
分别是 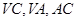 的中点,
的中点,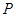 为
为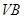 上任意一点,则直线
上任意一点,则直线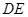 与
与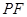 所成的角的大小是( )
所成的角的大小是( )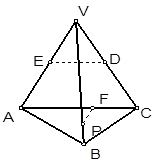





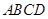 中,
中,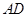 ∥
∥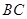 ,
,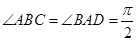 ,
,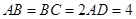 ,
,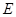 、
、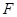 分别是
分别是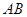 、
、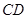 上的点,
上的点,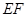 ∥
∥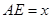 ,
,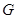 是
是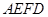 ⊥平面
⊥平面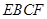 (如图).
(如图).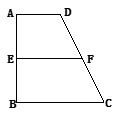
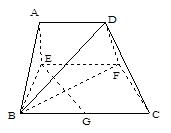
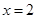 时,求证:
时,求证: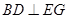 ;
;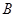 、
、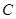 、
、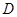 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为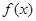 ,求
,求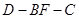 的余弦值.
的余弦值.