Question

如图，正三棱柱ABC-A₁B₁C₁中，D为线段A₁C₁中点．
（Ⅰ）求证：BC₁∥平面AB₁D；
（Ⅱ）若AA₁=

3

，二面角A-B₁D-A₁的大小为60⁰，求线段 AB 的长度．

Answer 1

分析：（Ⅰ）连A₁B交AB₁于点E，由题意可得：E为AB₁的中点，即可得到BC₁∥DE，进而利用线面平行的判定定理得到线面平行．
（Ⅱ）结合题中的条件建立空间直角坐标系，设AB=a，再写出各点的坐标，即可求出两个平面的法向量，进而利用向量之间的有关运算求出两个向量的夹角，再将其转化为二面角的平面角．

解答：证明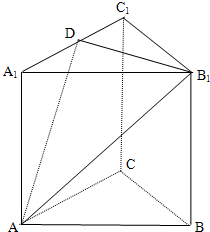：（Ⅰ）连A₁B交AB₁于点E，
∵四边形A₁ABB₁为矩形，
∴E为AB₁的中点…．（1分）
又D为线段A₁C₁中点，
∴BC₁∥DE…..（3分）
∵BC₁?平面AB₁D，DE?平面AB₁D．
∴BC₁∥平面AB₁D…..（6分）
解：（Ⅱ）以点A为原点，AB为X轴正半轴，平面ABC内过A垂直于AB的直线为Y轴，AA₁为Z轴，建立空间直角坐标系，设AB=a，
则A（0，0，0），A₁（0，0，

3

），B₁（a，0，

3

），D（

a

4

，

3

4

a，

3

)，
∴

AB1

=(a，0，

3

)，

AD

=

a

4

，

3

2

，

3

)，
设

n

=(x，y，z)⊥平面AB₁D，则

n

⊥

AB1

，

n

⊥

AD

，
故

n

•

AB1

=0，

n

•

AD

=0，
则ax+0+

3

z=0，

a

4

x+

3

4

ay+

3

z=0，
解得：y=

3

x，z=-

3

3

ax，
取

n=

(1，

3

，-

3

3

a)…．（9分）
∵AA₁⊥平面A₁B₁C₁，
∴

AA1

=(0，0，

3

)是平面A₁B₁C₁的一个法向量，
∴cos?

n

，

AA1

＞=

n • AA1

| n |•| AA1 |

=

-a

4+ 1 3 a2 • 3

=-

1

2

，
解得a=2，
∴线段 AB 的长度为2．…（12分）

点评：解决此类问题的关键是熟练则线面平行的判定定理与几何体的结构特征，对于求二面角的平面角的知识点，其关键是做角，一般是结合图形的结构及题设条件正确作出平面角来，也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角等问题