题目内容
15.在立方体ABCD-A1B1C1D1中,已知E1为A1D1的中点,求二面角E1-AB-C的大小.分析 由题意画出图形,找出二面角E1-AB-C的平面角,求解直角三角形得答案.
解答 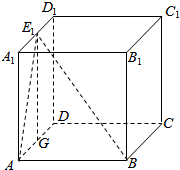 解:如图,
解:如图,
在正方体ABCD-A1B1C1D1中,由AB⊥面ADD1A1,
∴E1A⊥AB,DA⊥AB,则∠E1AD为二面角E1-AB-C的平面角.
∵E1为A1D1的中点,过E1作E1G⊥AD,垂足为G,
设正方体ABCD-A1B1C1D1的棱长为a,
则${E}_{1}G=a,AG=\frac{a}{2}$,
∴tan$∠{E}_{1}AG=\frac{a}{\frac{a}{2}}=2$.
∴二面角E1-AB-C的大小是arctan2.
点评 本题考查二面角的求法,正确找出二面角的平面角是关键,是中档题.

练习册系列答案
相关题目
10.已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-$\frac{1}{2}$的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |