题目内容
(本题满分13分)
检测部门决定对某市学校教室的 空气质量进行检测,空气质量分为A、B、C三级.
空气质量进行检测,空气质量分为A、B、C三级.
每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为 ,
, ,
, .
.
(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
检测部门决定对某市学校教室的
 空气质量进行检测,空气质量分为A、B、C三级.
空气质量进行检测,空气质量分为A、B、C三级.每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为
 ,
, ,
, .
.(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
解:(1)该间教室两次检测中,空气质量均为A级的概率为 ×
× =
=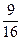 ,
,
该间教室两次检测中,空气质量一次为A级,另一次为B级的概率为2× ×
× =
=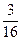 ,
,
设“该间教室的空气质量合格”为事件E,则 P(E)= ×
× +2×
+2× ×
× =
= .
.
故估计该间教室的空气质量合格的概率为 .
.
(2)法一:由题意可知,X的取值0,1,2,3,4.
P(X=i)=C4( )i(1-
)i(1- )4-i(i=0,1,2,3,4).
)4-i(i=0,1,2,3,4).
随机变量X的分布列为:
∴E(X)=0×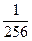 +1×
+1× +2×
+2×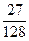 +3×
+3× +4×
+4×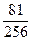 =3.
=3.
法二:∵X~B(4, ),∴E(X)=4×
),∴E(X)=4× =3.
=3.
 ×
× =
=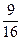 ,
,该间教室两次检测中,空气质量一次为A级,另一次为B级的概率为2×
 ×
× =
=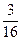 ,
,设“该间教室的空气质量合格”为事件E,则 P(E)=
 ×
× +2×
+2× ×
× =
= .
.故估计该间教室的空气质量合格的概率为
 .
.(2)法一:由题意可知,X的取值0,1,2,3,4.
P(X=i)=C4(
 )i(1-
)i(1- )4-i(i=0,1,2,3,4).
)4-i(i=0,1,2,3,4).随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 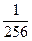 |  | 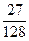 |  | 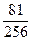 |
∴E(X)=0×
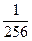 +1×
+1× +2×
+2×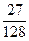 +3×
+3× +4×
+4×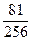 =3.
=3.法二:∵X~B(4,
 ),∴E(X)=4×
),∴E(X)=4× =3.
=3.略

练习册系列答案
相关题目

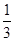
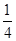
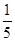

 (0<a<1),三各射击一次,击中目标的次数记为
(0<a<1),三各射击一次,击中目标的次数记为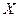 。
。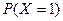 的值最大,求实数a的取值范围。
的值最大,求实数a的取值范围。 别写着数字1,2,3,5。同时投掷这两枚玩具一次,记
别写着数字1,2,3,5。同时投掷这两枚玩具一次,记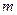 为两个朝下的面上的数字之和。
为两个朝下的面上的数字之和。 ,
,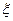 ,求
,求 。
。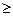 10的概率;
10的概率;