题目内容
【题目】如图,多面体![]() 中,
中,![]() ,平面
,平面![]() ⊥平面
⊥平面![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ∥
∥![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
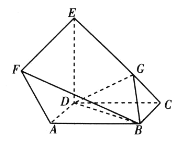
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)若![]() ,求多面体
,求多面体![]() 被平面
被平面![]() 分成的大、小两部分的体积比.
分成的大、小两部分的体积比.
【答案】(1)证明见解析(2) 11:1
【解析】
(1)由勾股定理逆定理证得![]() ,再由面面垂直的性质定理得线面垂直;
,再由面面垂直的性质定理得线面垂直;
(2)连接EB,AE. 多面体![]() 被分为
被分为![]() 四个三棱锥,由它们之间的体积关系可求得比值.
四个三棱锥,由它们之间的体积关系可求得比值.
(1)因为四边形ABCD为矩形,所以CD=AB.
因为AB=DE=2,所以CD=DE=2.
因为点G在线段CE上,且EG=2GC=![]() AB,所以EC=
AB,所以EC=![]() AB=
AB=![]() CD=
CD=![]()
所以![]() ,即
,即![]()
又平面CDE⊥平面ABCD,平面CDE![]() 平面ABCD=CD,DE
平面ABCD=CD,DE![]() 平面CDE,
平面CDE,
所以DE⊥平面ABCD.
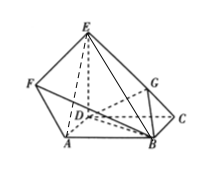
(2)设三棱锥G-BCD的体积为1,连接EB,AE.
因为EG=2GC,所以CG=![]() EC,所以
EC,所以![]() .
.
易知![]()
又EF=2BC,BC∥EF,所以![]() ,故
,故![]()
又![]() ,所以
,所以![]()
故![]()
故多面体ABCDEF被平面BDG分成的大、小两部分的体积比为11:1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目