题目内容
【题目】设A，B是椭圆C： 
+ 
=1长轴的两个端点，若C上存在点M满足∠AMB=120°，则m的取值范围是（ ）
A.（0，1]∪[9，+∞）
B.（0， 
]∪[9，+∞）
C.（0，1]∪[4，+∞）
D.（0， ]∪[4，+∞）
【答案】A
【解析】解：假设椭圆的焦点在x轴上，则0＜m＜3时，
假设M位于短轴的端点时，∠AMB取最大值，要使椭圆C上存在点M满足∠AMB=120°，
∠AMB≥120°，∠AMO≥60°，tan∠AMO= 
≥tan60°= 
，
解得：0＜m≤1；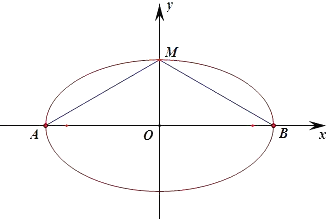
当椭圆的焦点在y轴上时，m＞3，
假设M位于短轴的端点时，∠AMB取最大值，要使椭圆C上存在点M满足∠AMB=120°，
∠AMB≥120°，∠AMO≥60°，tan∠AMO= 
≥tan60°= ，解得：m≥9，
∴m的取值范围是（0，1]∪[9，+∞）
故选A．
练习册系列答案
相关题目
