题目内容
设b>0，二次函数y＝ax2＋bx＋a2－1的图像为下列之一，则a的值为( )
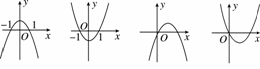
A．1 B．－1
C.
D.
B
解析 ∵b>0，∴－
≠0，故图像不可能为前两个，而后两个均过(0,0)点．
∴由a2－1＝0，得a＝±1.
又第三个图中－>0，－
>0，∴a＝－1.
而第四个图中－>0，－<0，不存在这样的a.
综上a＝－1.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
2, a2=
2, …, an=
2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
=1,n=3. 点P1(3,0) 及S3=255, 求点P3的坐标；
(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值；
2, a2=
2, …, an=
2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
－y2=1,n=3. 点P1(3,0) 及S3=162, 求点P3的坐标；
(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.设P1（x1,y1）, P1（x2,y2）,…, Pn（xn,yn）（n≥3,n∈N） 是二次曲线C上的点, 且a1=
2, a2=
2, …, an=
2构成了一个公差为d（d≠0） 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.
（1）若C的方程为
－y2=1,n=3. 点P1（3,0） 及S3=162, 求点P3的坐标；（只需写出一个）
（2）若C的方程为y2=2px（p≠0）. 点P1（0,0）, 对于给定的自然数n, 证明：（x1+p）2, （x2+p）2, …,（xn+p）2成等差数列；
（3）若C的方程为
（a>b>0）. 点P1（a,0）, 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.
| 符号意义 | 本试卷所用符号 | 等同于《实验教材》符号 |
| 向量坐标 |
|
|
| 正切 | tg | tan |
={x,y}
)；