题目内容
【题目】设![]() 为数列
为数列![]() 的前
的前![]() 项和,对任意的
项和,对任意的![]() ,都有
,都有![]() (
(![]() 为正常数).
为正常数).
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)利用![]() 与
与![]() 之间的关系
之间的关系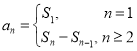 ,对
,对![]() 分两种情况讨论,
分两种情况讨论,![]() 时,求
时,求![]() 的值,
的值,![]() 时,利用
时,利用![]() 得出
得出![]() 与
与![]() 之间的关系,进而利用定义证明数列
之间的关系,进而利用定义证明数列![]() 为等比数列;
为等比数列;
(2)在(1)的条件下求出![]() 的值,然后根据数列
的值,然后根据数列![]() 的递推公式的结构利用倒数法得到数列
的递推公式的结构利用倒数法得到数列![]() 为等差数列,通过求处等差数列
为等差数列,通过求处等差数列![]() 的通项公式求出数列
的通项公式求出数列![]() 的通项公式;(3)利用(2)中数列
的通项公式;(3)利用(2)中数列![]() 的通项公式,并根据数列
的通项公式,并根据数列![]() 的通项公式的结构选择错位相减法求数列
的通项公式的结构选择错位相减法求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)证明:当![]() 时,
时,![]() ,解得
,解得![]() . 1分
. 1分
当![]() 时,
时,![]() .即
.即![]() . 2分
. 2分
又![]() 为常数,且
为常数,且![]() ,∴
,∴![]() . 3分
. 3分
∴数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列. 4分
的等比数列. 4分
(2)![]() 5分 ∵
5分 ∵![]() ,∴
,∴![]()
![]() ,即
,即![]() . 7分
. 7分
∴![]() 是首项为
是首项为![]() ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分
∴![]() ,即
,即![]() . 9分
. 9分
(3)由(2)知![]() ,则
,则![]() .
.
所以![]() , 10分
, 10分
即![]() , ① 11分
, ① 11分
则![]() , ② 12分
, ② 12分
②-①得![]() , 13分
, 13分
故![]() . 14分
. 14分

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目