题目内容
【题目】已知椭圆的两个焦点为 ![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若 ![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线l过右焦点 ![]() (不与x轴重合)且与椭圆相交于不同的两点A,B,在x轴上是否存在一个定点P(x0 , 0),使得
(不与x轴重合)且与椭圆相交于不同的两点A,B,在x轴上是否存在一个定点P(x0 , 0),使得 ![]() 的值为定值?若存在,写出P点的坐标(不必求出定值);若不存在,说明理由.
的值为定值?若存在,写出P点的坐标(不必求出定值);若不存在,说明理由.
【答案】
(1)解:由题意椭圆的焦点在x轴上, ![]() (a>b>0),
(a>b>0),
c= ![]() ,|
,| ![]() |2+|
|2+| ![]() |2=(2c)2=20,|
|2=(2c)2=20,| ![]() ||
|| ![]() |=8
|=8
∴(| ![]() |+|
|+| ![]() |)2=|
|)2=| ![]() |2+|
|2+| ![]() |2+2|
|2+2| ![]() ||
|| ![]() |=36 解得:|
|=36 解得:| ![]() |+|
|+| ![]() |=6,
|=6,
2a=6,则a=3 b2=a2﹣c2=4
∴椭圆的方程为: ![]()
(2)解:解法一:设直线l的方程为:x=my+ ![]() ,
,
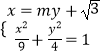 ,并消元整理得:(4m2+9)x2﹣18
,并消元整理得:(4m2+9)x2﹣18 ![]() x+45﹣36m2=0,…①
x+45﹣36m2=0,…①
设A(x1,y1),B(x2,y2),则是方程①的两个解,由韦达定理得:
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,y1y2=
,y1y2= ![]() (x1﹣
(x1﹣ ![]() )(x2﹣
)(x2﹣ ![]() )=
)= ![]() ( x1x2﹣
( x1x2﹣ ![]() (x1+x2)+5)=﹣
(x1+x2)+5)=﹣ ![]() ,
,
![]()
![]() =(x1﹣x0,y1)(x2﹣x0,y2)=( x1﹣x0)( x2﹣x0)+y1y2=x1x2﹣x0(x1+x2)+x02+y1y2
=(x1﹣x0,y1)(x2﹣x0,y2)=( x1﹣x0)( x2﹣x0)+y1y2=x1x2﹣x0(x1+x2)+x02+y1y2
= ![]() ﹣
﹣ ![]() ×x0+x02+(﹣
×x0+x02+(﹣ ![]() )=
)= ![]() ,
,
令 ![]()
![]() =t 则(4x02﹣36)m2+9x02﹣18
=t 则(4x02﹣36)m2+9x02﹣18 ![]() x0+29=t(4m2+9),
x0+29=t(4m2+9),
比较系数得:4x02﹣36=4t且9x02﹣18 ![]() x0+29=9t 消去t得:36x02﹣36×9=36x02﹣72
x0+29=9t 消去t得:36x02﹣36×9=36x02﹣72 ![]() x0+29×4 解得:x0=
x0+29×4 解得:x0= ![]() ,
,
∴在x轴上存在一个定点P( ![]() ,0),使得
,0),使得 ![]()
![]() 的值为定值(﹣
的值为定值(﹣ ![]() );
);
解法二:当直线与x轴不垂直时,设直线l方程为:y=k(x﹣ ![]() ),代入椭圆方程并消元整理得:
),代入椭圆方程并消元整理得:
(9k2+4)x2﹣18 ![]() k2x+45k2﹣36=0…①
k2x+45k2﹣36=0…①
设A(x1,y1),B(x2,y2),则是方程①的两个解,由韦达定理得:
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
y1y2=k2(x1﹣ ![]() )(x2﹣
)(x2﹣ ![]() )=k2( x1x2﹣
)=k2( x1x2﹣ ![]() (x1+x2)+5)=﹣
(x1+x2)+5)=﹣ ![]() ,
,
![]()
![]() =(x1﹣x0,y1)(x2﹣x0,y2)=( x1﹣x0)( x2﹣x0)+y1y2=x1x2﹣x0(x1+x2)+x02+y1y2,
=(x1﹣x0,y1)(x2﹣x0,y2)=( x1﹣x0)( x2﹣x0)+y1y2=x1x2﹣x0(x1+x2)+x02+y1y2,
= ![]() ,
,
令 ![]()
![]() =t 则(9x02﹣18
=t 则(9x02﹣18 ![]() x0+29)k2+4x02﹣36=t(4+9k2),
x0+29)k2+4x02﹣36=t(4+9k2),
9x02﹣18 ![]() x0+29=9 t且 4x02﹣36=4t,
x0+29=9 t且 4x02﹣36=4t,
解得:x0= ![]() ,此时t的值为﹣
,此时t的值为﹣ ![]() ,
,
当直线l与x轴垂直时,l的方程为:x= ![]() ,代入椭圆方程解得:A(
,代入椭圆方程解得:A( ![]() ,﹣
,﹣ ![]() ),B(
),B( ![]() ,
, ![]() ),
),
![]()
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() )(﹣
)(﹣ ![]() ,
, ![]() )=
)= ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
∴当直线l与x轴垂直时, ![]()
![]() 也为定值﹣
也为定值﹣ ![]() ,
,
综上,在x轴上存在一个定点P( ![]() ,0),使得
,0),使得 ![]()
![]() 的值为定值(﹣
的值为定值(﹣ ![]() )
)
【解析】(1)根据椭圆的定义及勾股定理即可求得a=3,c= ![]() ,b2=a2﹣c2=4,即可求得椭圆方程;(2)方法一:设直线l:x=my+
,b2=a2﹣c2=4,即可求得椭圆方程;(2)方法一:设直线l:x=my+ ![]() ,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,
,代入椭圆方程,利用韦达定理及向量数量积的坐标运算, ![]()
![]() =t 则(4x02﹣36)m2+9x02﹣18
=t 则(4x02﹣36)m2+9x02﹣18 ![]() x0+29=t(4m2+9),比较系数,即可求得x0=
x0+29=t(4m2+9),比较系数,即可求得x0= ![]() ,在x轴上存在一个定点P(
,在x轴上存在一个定点P( ![]() ,0),使得
,0),使得 ![]()
![]() 的值为定值(﹣
的值为定值(﹣ ![]() ); 方法二:分类讨论,当直线l的斜率存在时,设直线l:y=k(x﹣
); 方法二:分类讨论,当直线l的斜率存在时,设直线l:y=k(x﹣ ![]() ),代入椭圆方程,利用韦达定理及向量数量积的坐标运算,令
),代入椭圆方程,利用韦达定理及向量数量积的坐标运算,令 ![]()
![]() =t 则(9x02﹣18
=t 则(9x02﹣18 ![]() x0+29)k2+4x02﹣36=t(4+9k2),9x02﹣18
x0+29)k2+4x02﹣36=t(4+9k2),9x02﹣18 ![]() x0+29=9 t且4x02﹣36=4t,即可求得x0=
x0+29=9 t且4x02﹣36=4t,即可求得x0= ![]() ,此时t的值为﹣
,此时t的值为﹣ ![]() .
.

【题目】甲、乙两人玩一种游戏,游戏规则如下:先将筹码放在如下表的正中间D处,投掷一枚质地均匀的硬币,若正面朝上,筹码向右移动一格;若反面朝上,筹码向左移动一格.
A | B | C | D | E | F | G |
30 | 5 | 10 | 10 | 5 | 20 | 30 |
(1)将硬币连续投掷三次,现约定:若筹码停在A或B或C或D处,则甲赢;否则,乙赢.问该约定对乙公平吗?请说明理由.
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定: ①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A﹣G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.


