题目内容
【题目】已知a>0,b∈R,函数f(x)=4ax2﹣2bx﹣a+b的定义域为[0,1].
(1)当a=1时,函数f(x)在定义域内有两个不同的零点,求b的取值范围;
(2)设f(x)的最大值和最小值分别为M和m,求证:M+m>0.
【答案】
(1)解:由题意可得f(x)=4x2﹣2bx﹣1+b在[0,1]内有两个不同的零点,
即有 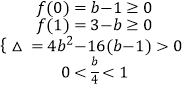 即为
即为 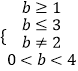 ,
,
解得1≤b<2或2<b≤3
(2)证明:f(x)的对称轴为x= ![]() ,
,
当 ![]() >1时,区间[0,1]为减区间,可得M=f(0)=b﹣a,
>1时,区间[0,1]为减区间,可得M=f(0)=b﹣a,
m=f(1)=3a﹣b,则M+m=2a>0;
当 ![]() <0时,区间[0,1]为增区间,可得m=f(0)=b﹣a,
<0时,区间[0,1]为增区间,可得m=f(0)=b﹣a,
M=f(1)=3a﹣b,则M+m=2a>0;
当0≤ ![]() ≤1时,区间[0,
≤1时,区间[0, ![]() ]为减区间,[
]为减区间,[ ![]() ,1]为增区间,
,1]为增区间,
可得m=f( ![]() )=
)= ![]() ,
,
若f(0)≤f(1),即b≤2a,可得M=f(1)=3a﹣b,
M+m= ![]() ≥
≥ ![]() =a>0;
=a>0;
若f(0)>f(1),即2a<b≤4a,可得M=f(0)=b﹣a,
M+m= ![]() =
= ![]() ,
,
由于2a<b≤4a,可得M+m∈(a,2a],即为M+m>0.
综上可得M+m>0恒成立
【解析】(1)由题意可得f(0)≥0,f(1)≥0,△>0,0< ![]() <1,解不等式即可得到所求范围;(2)求出对称轴,讨论对称轴和区间[0,1]的关系,可得最值,即可证明M+m>0.
<1,解不等式即可得到所求范围;(2)求出对称轴,讨论对称轴和区间[0,1]的关系,可得最值,即可证明M+m>0.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


