题目内容

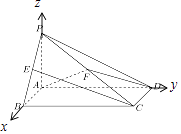
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PB、PD与
平面ABCD所成的角依次是 和 ，AP=2，E、F依次是PB、PC的中点；

（1）求异面直线EC与PD所成角的大小；（结果用反三角函数值表示）
（2）求三棱锥P﹣AFD的体积．

【答案】
（1）解：分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系．

∵AP=2， ，∠PDA= ，

∴AB=2，AD=4，则P（0，0，2），D（0，4，0），E（1，0，1），C（2，4，0），

， ．

∴cos＜ ＞= = = ．

∴异面直线EC与PD所成角的大小为


（2）解：VP﹣AFD=VP﹣ACD﹣VF﹣ACD= = ．
【解析】（1）分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系．利用向量 与 所成角求得异面直线EC与PD所成角的大小；（2）直接利用VP﹣AFD=VP﹣ACD﹣VF﹣ADC求解．
【考点精析】认真审题，首先需要了解异面直线及其所成的角(异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系)．

练习册系列答案
相关题目

【题目】已知数列{an}满足：a1=1，an= ，n=2，3，4，…．
（1）求a2 ， a3 ， a4 ， a5的值；
（2）设bn= +1，n∈N*，求证：数列{bn}是等比数列，并求出其通项公式；
（3）对任意的m≥2，m∈N*，在数列{an}中是否存在连续的2m项构成等差数列？若存在，写出这2m项，并证明这2m项构成等差数列；若不存在，请说明理由．

【题目】为了解市民在购买食物时看营养说明与性别的关系，现在社会上随机询问了100名市民，得到如下2×2列联表：
（1）是否有95%的把握认为：“性别与读营养说明有关系”，并说明理由；
（2）把频率当概率，若从社会上的男性市民中随机抽取3位，记这3位中读营养说明的人数为ξ，求随机变量ξ的分布列和数学期望E（ξ）．

男性

女性

总计

读营养说明

40

20

60

不读营养说明

20

20

40

总计

60

40

100

参考公式和数据：

P（K2≥k0）

0.10

0.050

0.025

0.010

k0

2.706

3.841

5.024

6.635

【题目】如图，F1 ， F2分别是椭圆C： =1（a＞b＞0）的左、右焦点，且焦距为2 ，动弦AB平行于x轴，且|F1A|+|F1B|=4．

（1）求椭圆C的方程；
（2）若点P是椭圆C上异于点 、A，B的任意一点，且直线PA、PB分别与y轴交于点M、N，若MF2、NF2的斜率分别为k1、k2 ， 求证：k1k2是定值．

【题目】设集合Ma={f（x）|存在正实数a，使得定义域内任意x都有f（x+a）＞f（x）}．
（1）若f（x）=2x﹣x2 ， 试判断f（x）是否为M1中的元素，并说明理由；
（2）若 ，且g（x）∈Ma ， 求a的取值范围；
（3）若 （k∈R），且h（x）∈M2 ， 求h（x）的最小值．

【题目】定义f（x）={x}（其中{x}表示不小于x的最小整数）为“取上整函数”，例如{2.1}=3，{4}=4．以下关于“取上整函数”性质的描述，正确的是（ ） ①f（2x）=2f（x）；
②若f（x1）=f（x2），则x1﹣x2＜1；
③任意x1 ， x2∈R，f（x1+x2）≤f（x1）+f（x2）；
④ ．
A.①②
B.①③
C.②③
D.②④

【题目】如图，已知椭圆C的中心为原点O，F（﹣2 ，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（ ）
A. =1
B. =1
C. =1
D. =1

【题目】(2015·江苏）已知集合X={1，2，3}，Yn={1,2,3...,n}(nN*)，Sn={(a,b)|a整除b或b整除a， aX, bYn}, 令f(n)表示集合Sn所包含元素的个数。
（1）写出f（6）的值；
（2）当n≥6时，写出f(n)的表达式，并用数学归纳法证明.

【题目】已知椭圆的两个焦点为 ， 是椭圆上一点，若 ， ．
（1）求椭圆的方程；
（2）直线l过右焦点 （不与x轴重合）且与椭圆相交于不同的两点A，B，在x轴上是否存在一个定点P（x0 ， 0），使得 的值为定值？若存在，写出P点的坐标（不必求出定值）；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网