题目内容
【题目】20世纪70年代,流行一种游戏﹣﹣﹣角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成 ![]() ,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4﹣2﹣1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4﹣2﹣1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( ) 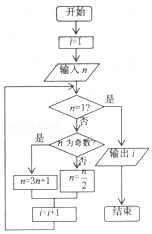
A.5
B.16
C.5或32
D.4或5或32
【答案】C
【解析】解:模拟程序的运行,由题意可得 当输入的n的值为5时,
i=1,第1次循环,n=5,n为奇数,n=16
i=2,第2次循环,n为偶数,n=8
i=3,第3次循环,n为偶数,n=4
i=4,第4次循环,n为偶数,n=2
i=5,第5次循环,n为偶数,n=1
i=6,满足条件n=1,退出循环,输出i的值为6.符合题意.
当输入的n的值为16时,
i=1,第1次循环,n=16,n为偶数,n=8
i=2,第2次循环,n为偶数,n=4
i=3,第3次循环,n为偶数,n=2
i=4,第4次循环,n为偶数,n=1
i=5,满足条件n=1,退出循环,输出i的值为5.不符合题意.
当输入的n的值为32时,
i=1,第1次循环,n=32,n为偶数,n=16
i=2,第2次循环,n为偶数,n=8
i=3,第3次循环,n为偶数,n=4
i=4,第4次循环,n为偶数,n=2
i=5,第5次循环,n为偶数,n=1
i=6,满足条件n=1,退出循环,输出i的值为6.符合题意.
当输入的n的值为4时,
i=1,第1次循环,n=4,n为偶数,n=2
i=2,第2次循环,n为偶数,n=1
i=3,满足条件n=1,退出循环,输出i的值为3.不符合题意.
故选:C.
根据各个选项n的值,模拟程序的运行,依次验证程序的输出的i的值是否为6即可得解.

 名校课堂系列答案
名校课堂系列答案