题目内容
20.根据表格内容填空:| x | -2 | 0 | 2 |
| y | 0 | -4 | 0 |
(2)写出所对应的一元二次方程的解±2;
(3)写出当y>0时的一元二次不等式的解集{x|x<-2,或x>2};;
(4)写出当y≤0时的一元二次不等式的解集{x|-2≤x≤2};;
(5)写出当y≤2时的一元二次不等式的解集{x|-$\sqrt{6}$≤x≤$\sqrt{6}$};;
(6)写出当y>1时的一元二次不等式的解集{x|x<-$\sqrt{5}$,或x>$\sqrt{5}$};.
分析 根据已知中函数图象过(-2,0)、(2,0)和(0,-4)点,利用待定系数法,可得函数的解析式,进而可得相应方程的解和相应不等式的解集.
解答 解:∵函数图象过(-2,0)和(2,0)点,
故设函数的解析式为y=a(x+2)(x-2),
将(0,-4)点代入得:
a=1,
故函数的解析式为y=(x+2)(x-2)=x2-4,
(1)故经过这些点的二次函数解析式为:y=x2-4;
(2)对应一元二次方程x2-4=0的解是:±2;
(3)y>0时,一元二次不等式x2-4>0的解集是:{x|x<-2,或x>2};
(4)y≤0时,一元二次不等式x2-4≤0的解集是:{x|-2≤x≤2};
(5)y≤2时,一元二次不等式x2-4≤2的解集是:{x|-$\sqrt{6}$≤x≤$\sqrt{6}$};
(6)y>1时,一元二次不等式x2-4>1的解集是:{x|x<-$\sqrt{5}$,或x>$\sqrt{5}$};
故答案为:y=x2-4;±2;{x|x<-2,或x>2}; {x|-2≤x≤2};{x|-$\sqrt{6}$≤x≤$\sqrt{6}$};{x|x<-$\sqrt{5}$,或x>$\sqrt{5}$};
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
10.关于实数x的不等式-x2+bx+c<0的解集是{x|x<-3或x>2},则关于x的不等式cx2-bx-1>0的解集是( )
| A. | (-$\frac{1}{2}$,$\frac{1}{3}$) | B. | (-2,3) | C. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,+∞) | D. | (-∞,-2)∪(3,+∞) |
15.函数f(x)=logax的图象如图所示,则a的取值可能是( )
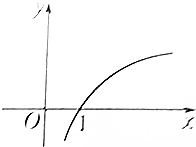
| A. | 10 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
5.已知函数f(x)=$\left\{\begin{array}{l}{2x-1(x>-1)}\\{{e}^{x}(x≤-1)}\end{array}\right.$,若a<b,f(a)=f(b),则实数a-2b的取值范围为( )
| A. | (-∞,$\frac{1}{e}$-1) | B. | (-∞,1-$\frac{1}{e}$) | C. | (-∞,2-$\frac{1}{e}$) | D. | (-∞,-$\frac{1}{e}$-2) |