题目内容
 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a( )
)(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数.
(2)求y=
 的最大值与最小值.
的最大值与最小值.
【答案】分析:(1)根据G是边长为1的正三角形ABC的中心,可求得AG,进而利用正弦定理求得GM,然后利用三角形面积公式求得S1,同理可求得S2
(2)把(1)中求得S1与S2代入求得函数的解析式,进而根据α的范围和余切函数的单调性求得函数的最大和最小值.
解答:解:(1)因为G是边长为1的正三角形ABC的中心,
所以AG=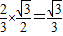 ,
,
∠MAG=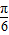 ,
,
由正弦定理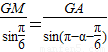
得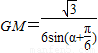
则S1= GM•GA•sina=
GM•GA•sina=
同理可求得S2=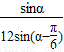
(2)y=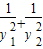 =
=
=72(3+cot2a)
因为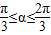 ,
,
所以当a=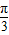 或a=
或a= 时,y取得最大值ymax=240
时,y取得最大值ymax=240
当a=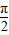 时,y取得最小值ymin=216
时,y取得最小值ymin=216
点评:本题主要考查了解三角形问题.考查了学生综合分析问题和解决问题的能力.
(2)把(1)中求得S1与S2代入求得函数的解析式,进而根据α的范围和余切函数的单调性求得函数的最大和最小值.
解答:解:(1)因为G是边长为1的正三角形ABC的中心,
所以AG=
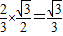 ,
,∠MAG=
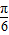 ,
,由正弦定理
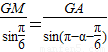
得
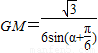
则S1=
 GM•GA•sina=
GM•GA•sina=
同理可求得S2=
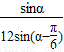
(2)y=
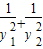 =
=
=72(3+cot2a)
因为
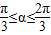 ,
,所以当a=
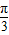 或a=
或a= 时,y取得最大值ymax=240
时,y取得最大值ymax=240当a=
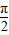 时,y取得最小值ymin=216
时,y取得最小值ymin=216点评:本题主要考查了解三角形问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
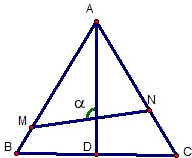 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a( 20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.
20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点. 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: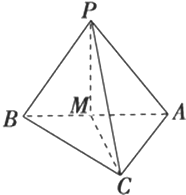 如图:已知△ABC是直角三角形,∠ACB=90°,M为AB的中点,PM⊥△ABC所在的平面,那么PA、PB、PC的大小关系是( )
如图:已知△ABC是直角三角形,∠ACB=90°,M为AB的中点,PM⊥△ABC所在的平面,那么PA、PB、PC的大小关系是( )