题目内容
 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:(1)FD∥平面ABC;
(2)AF⊥平面EDB.
分析:(1)要证FD∥平面ABC,可以通过证明FD∥MC实现.而后者可以通过证明CD∥FM,CD=FM,证明四边形FMCD是平行四边形而得出.
(2)要证AF⊥平面EDB,可以通过证明AF⊥EB,AF⊥FD实现.AF⊥EB易证,而AF⊥FD可通过CM⊥面EAB,结合CM∥FD证出.
(2)要证AF⊥平面EDB,可以通过证明AF⊥EB,AF⊥FD实现.AF⊥EB易证,而AF⊥FD可通过CM⊥面EAB,结合CM∥FD证出.
解答:证明(1)∵F分别是BE的中点,取BA的中点M,
∴FM∥EA,FM=
EA=a
∵EA、CD都垂直于平面ABC,∴CD∥EA,
∴CD∥FM,又CD=a=FM
∴四边形FMCD是平行四边形,∴FD∥MC,
FD?平面ABC,MC?平面ABC
∴FD∥平面ABC.
(2)因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 EA垂直于平面ABC∴CM⊥AE,
又 AE∩AB=A,所以CM⊥面EAB,∵AF?面EAB
∴CM⊥AF,又CM∥FD,从而FD⊥AF,
因F是BE的中点,EA=AB所以AF⊥EB.
EB,FD是平面EDB内两条相交直线,所以AF⊥平面EDB.
∴FM∥EA,FM=
| 1 |
| 2 |
∵EA、CD都垂直于平面ABC,∴CD∥EA,
∴CD∥FM,又CD=a=FM
∴四边形FMCD是平行四边形,∴FD∥MC,
FD?平面ABC,MC?平面ABC
∴FD∥平面ABC.
(2)因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 EA垂直于平面ABC∴CM⊥AE,
又 AE∩AB=A,所以CM⊥面EAB,∵AF?面EAB
∴CM⊥AF,又CM∥FD,从而FD⊥AF,
因F是BE的中点,EA=AB所以AF⊥EB.
EB,FD是平面EDB内两条相交直线,所以AF⊥平面EDB.
点评:本题考查空间直线和平面的位置关系,考查空间想象能力、转化、论证能力.

练习册系列答案
相关题目
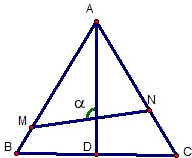 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a( 20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.
20、如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点.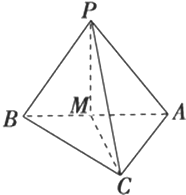 如图:已知△ABC是直角三角形,∠ACB=90°,M为AB的中点,PM⊥△ABC所在的平面,那么PA、PB、PC的大小关系是( )
如图:已知△ABC是直角三角形,∠ACB=90°,M为AB的中点,PM⊥△ABC所在的平面,那么PA、PB、PC的大小关系是( )