Question

4．如图，在边长为2的正方体ABCD-A₁B₁C₁D₁中，P为棱AB的中点，M为面BCC₁B₁上的点．一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点D₁．则线段PM与线段MD₁的长度和为（　　）

• A． $\sqrt{15}$
• B． 4
• C． $\sqrt{17}$
• D． 3$\sqrt{2}$

Answer 1

分析 利用正方体的几何性质，光的反射原理，根据对称性，得出线段PM与线段MD₁的长度和等于线段D₁N的长度，利用直角三角形Rt△D₁DN，求解即可．

解答 解：根据几何体的性质，结合光的反射原理得出
P关于B的对称点N，
∴MP=NP，
即连接DN，D₁N，
根据正方体的性质，得出Rt△D₁DN，
∵边长为2，
∴AN=3，AD=2，
即DN=$\sqrt{13}$，
∵DD₁=2，
∴D₁N=$\sqrt{13+4}$=$\sqrt{17}$．
故选：C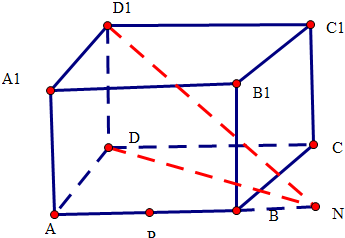

点评 本题考查了正方体的几何性质，光的反射原理，对称性问题，化折线为直线求解线段的长度，题目很新颖，属于中档题．